大学物理期末急救指北

刚体

平动和转动的迅速沟通

	质点	刚体
运动方程	$F=ma$	$M=J\alpha$
动量/角动量	$p=mv$	$L=J\omega=mvr$
动量/角动量定理	$\int F\mathrm dt=\Delta p$	$\int M\mathrm dt=\Delta L$
动能	$E_k=\frac 12 mv^2$	$E_k=\frac 12 J\omega^2$
力/力矩做功	$W=\int F\mathrm dx$	$W=\int M\mathrm d\theta$

转动惯量

$$\begin{gather} J=\sum m_ir_i^2=\int r^2\mathrm dm \end{gather}$$

质量分布离轴越远，转动惯量越大。空心物体比实心物体转动惯量大。

常见物体的转动惯量

形状	转动惯量
圆环、空心圆柱	$MR^2$
圆盘、实心圆柱	$\frac12 MR^2$
细杆（绕中点）	$\frac 1{12} ML^2$
细杆（绕端点）	$\frac 13 ML^2$

平行轴定理

刚体对于任意轴的转动惯量=对于质心的转动惯量+质量乘以两个轴距离的平方

$$\begin{gather} J=J_c+md^2 \end{gather}$$

也就是换轴需要借助质心来换。

转动定律

角加速度 $a$ 正比于合外力矩 $M=Fd$ ，反比于转动惯量 $J=mL^2$。

$$\begin{align} M&=Fd\\ M&=Ja \end{align}$$

刚体的角动量守恒

角动量

$$\begin{gather} L=J\omega \end{gather}$$

角动量定理

外力矩对时间的积累等于角动量的变化

$$\begin{gather} \int_{t_1}^{t_2} M_外\mathrm dt=J\omega_2-J\omega_1 \end{gather}$$

角动量守恒定律

若外力矩为零，则角动量 $L=J\omega$ 不变。

若刚体绕着光滑轴旋转，无其他外力，则角动量守恒。

例：人质量m在半径R的水平平台边缘，平台可绕其中心的竖直光滑固定轴旋转，转动惯量为J。平台和人静止。突然人以相对地面为v的速率在边缘逆时针转动行走，求此视平台对于地面旋转角速度

角动量守恒，且为零。

$$\begin{gather} 0=J\cdot w+m\cdot vR\\ \therefore \omega=-\frac{mvR}{J} \end{gather}$$

解释：角速度大小为 $\frac{mvR}{J}$，方向与人行走方向相反。

---

刚体的动能

$$\begin{gather} E_k=\frac12 J\omega^2 \end{gather}$$

静电场

电荷

电荷激发电场

$$Q=ne\quad e\approx1.602\times10^{-19}\rm C$$

孤立系统种总电荷量不变（正负电荷代数和不变）

库伦定律

$$\begin{gather} \vec{F_{21}}=\frac{1}{4\pi \varepsilon_0}\frac{q_1q_2}{r^2}\vec{r_{21}} \end{gather}$$

通常会令 $k=\frac{1}{4\pi \varepsilon_0}$ 以简写，但是 $\pi \varepsilon_0$​ 出现频率挺高的。

$\varepsilon_0$ 是真空中的电介质常数，也称为真空电容率，其值约为 $8.85 \times 10^{-12}$ 法拉/米（F/m）。

多个点电荷则矢量叠加，带电导体则积分。

$$\begin{gather} \vec{E}=\frac{\vec{F}}{q_0} \end{gather}$$

场强：大小为单位电荷在该点受力的大小，方向为正电荷在该点受力方向。

点电荷的电场

$$\begin{gather} \vec{E}=\frac{\vec F}{q_0}=\frac{1}{4\pi \varepsilon_0}\frac{q}{r^2}\vec {r^0} \end{gather}$$

连续分布的带电体

$$\begin{gather} \mathrm d\vec E=\frac{1}{4\pi \varepsilon_0}\frac{\mathrm dq}{r^2}\vec{r^0}\\ \vec E=\int\frac{\mathrm dq}{4\pi \varepsilon_0r^2}\vec{r^0}\\ \end{gather}$$

其中

$$\mathrm dq= \begin{cases} \lambda \mathrm dl&(体分布)&\lambda:线密度\\ \sigma \mathrm dS&(体分布)&\sigma:面密度\\ \rho \mathrm dV&(体分布)&\rho:体密度 \end{cases}$$

---

例：长为L的均匀带电直杆，电荷线密度为$\lambda$，求其在空间一点P产生的电场强度，P到杆的垂直距离为a

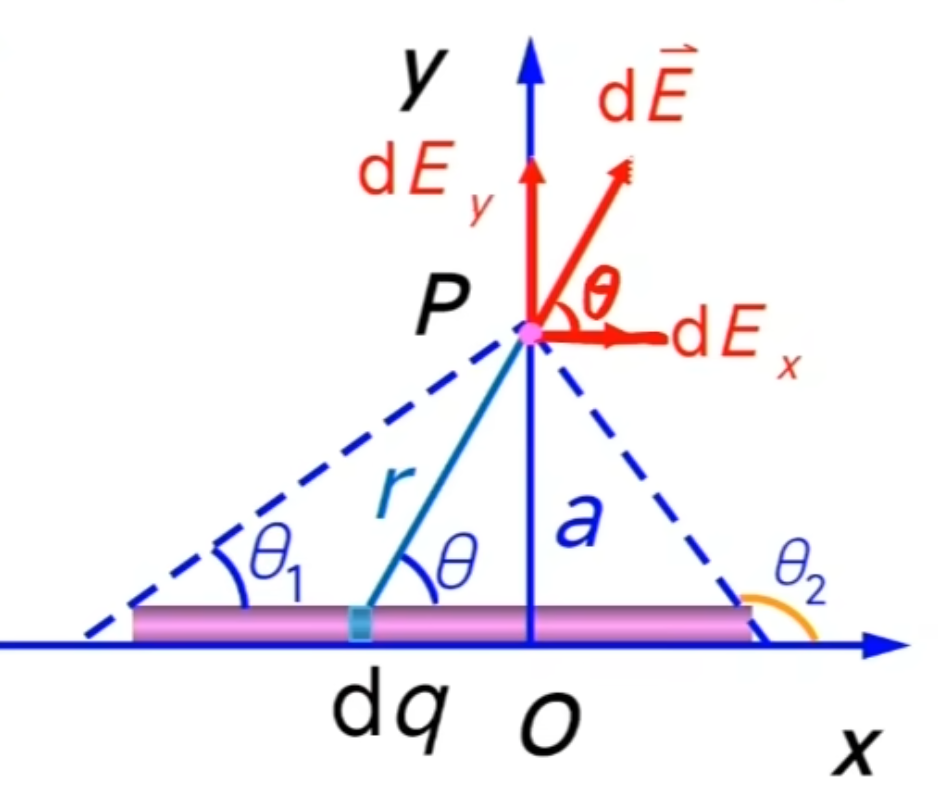$$\begin{gather} \mathrm dq=\lambda \mathrm dx\\ \mathrm dE=\frac{1}{4\pi \varepsilon_0}\frac{\lambda\mathrm dx}{r^2}\\ \mathrm dE_x=\mathrm dE\cos\theta\\ \mathrm dE_y=\mathrm dE\sin\theta\\ x=a\tan(\theta-\frac{\pi}{2})=-a\cot\theta\\ \mathrm dx=a\csc^2\theta \mathrm d\theta\\ \nonumber\\ E_x=\int \mathrm dE_X=\int_{\theta_1}^{\theta_2}\frac{\lambda}{4\pi \varepsilon_0a}\cos\theta\mathrm d\theta\\ =\frac{\lambda}{4\pi\varepsilon_0a}(\sin\theta_2-\sin\theta_1)\\ \nonumber\\ E_y=\frac{\lambda}{4\pi\varepsilon_0a}(\cos\theta_2-\cos\theta_1) \end{gather}$$

考试一般不考这种复杂的、位置不确定的。

带电杆的较远处的场强

杆可以看成点电荷，$\theta_1=\theta_2$，所以有

$$\begin{gather} E_x=0,E_y=\frac{\lambda L}{4\pi \varepsilon_0a^2}=\frac{1}{4\pi \varepsilon_0}\frac{\lambda L}{a^2} \end{gather}$$

无限长直导线场强

$\theta_1=0,\theta_2=180^\circ$

$$\begin{gather} E_x=0,E_y=\frac{\lambda}{2\pi \varepsilon_0a} \end{gather}$$

---

例：半径为R的均匀带电圆环，带电量q。求圆环周先上任意一点P的电场强度

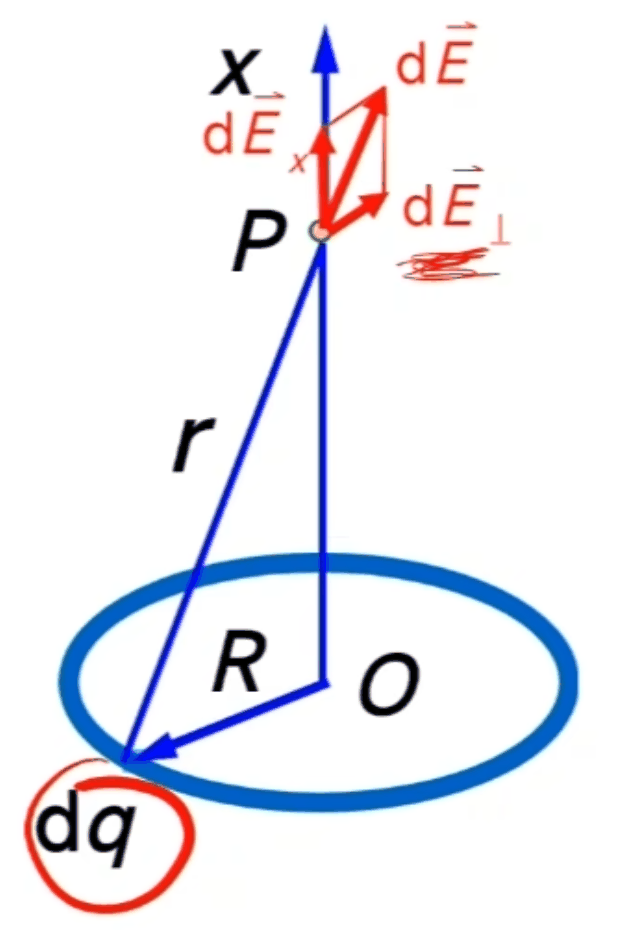$$\begin{gather} \mathrm dq=\lambda \mathrm dl\\ \mathrm dE=\frac{1}{4\pi \varepsilon_0}\frac{\mathrm dq}{r^2}\\ \mathrm dE_\perp=0(对称性)\\ \mathrm dE_x=\mathrm dE\cos \theta \end{gather}$$ $$\begin{align} E_x&=\frac{1}{4\pi\varepsilon_0}\int\frac{\mathrm dq}{r^2}\cos\theta\\ &=\frac{1}{4\pi \varepsilon_0}\frac{\cos\theta}{r^2}\int\mathrm dq\\ &=\frac{1}{4\pi \varepsilon_0}\frac{\cos\theta}{r^2}q\\ &=\frac{1}{4\pi \varepsilon_0}\frac{qx}{(R^2+x^2)^{\frac32}} \end{align}$$

带电圆环在圆心处场强

$E=0$

带电圆环在无穷远处场强

$x\gg R$，可以将圆环视作点电荷，$E=\frac1{4\pi\varepsilon_0}\frac{q}{x^2}$​

---

例：面密度为$\sigma$的圆板在轴线上任一点的电场强度

之前是$\mathrm dq$在$L$上积分，所以$\mathrm dq=\lambda \mathrm dl$

在板子上，是以一个环作为一个小量进行积分。

每个小环=环的周长乘以环的宽度$\mathrm dr$

$$\begin{gather} \mathrm dq=2\pi r\mathrm dr \end{gather}$$

或者，$\mathrm dq=\sigma\mathrm dS=\sigma\mathrm d(\pi r^2)$，本质上是一样的。

$$\begin{gather} \mathrm dE=\frac1{4\pi \varepsilon_0}\frac{x\mathrm dq}{(r^2+x^2)^\frac32}\\ E=\int \mathrm dE= \frac{x\sigma}{2\varepsilon_0}\int_0^R\frac{r\mathrm dr}{(r^2+x^2)^\frac32}\\ =\frac \sigma {2\varepsilon_0}[1-\frac{x}{(R^2+x^2)^\frac12}] \end{gather}$$

电场线与电通量

• 由正电荷指向负电荷或无穷远处
• 切线反映方向，疏密反映场强大小
• 非闭合曲线
• 不相交

电通量：穿过曲面S的电场线条数

$$\begin{gather} \mathrm d\phi_e=E_n\mathrm dS=E\cos\theta\mathrm dS=E\mathrm dS_\perp \end{gather}$$

非均匀场：对S积分

$$\begin{gather} \phi_e=\int \mathrm d\phi_e=\int_S\vec E\cdot \mathrm d\vec S \end{gather}$$

高斯定理

$$\begin{gather} \phi_e=\oint_S\vec E\cdot \mathrm d\vec S=\frac 1 {\varepsilon_0}\sum_i q_i=\frac1{\varepsilon_0}\int_V \rho\mathrm dV \end{gather}$$

穿过闭合曲面的电通量在数值上等于曲面内包围的电量的代数和乘以$\frac1{\varepsilon_0}$

例：均匀带电球面，总电量Q，半径R。求某点处E

对于球面外一点P：

取过P的同心求面为高斯面，表面积$4\pi r^2$。对于高斯面上每一个dS，都会有大小为E的场强穿过。

$$\begin{gather} \phi_e=\oint_S \vec E\cdot \mathrm d\vec S=\oint_S E\mathrm dS=E\oint_S\mathrm dS=E\cdot 4\pi r^2\\ \phi_e=\frac1{\varepsilon_0}\sum_i q_i=\frac1{\varepsilon_0}Q\\ \therefore E=\frac{Q}{4\pi\varepsilon_0 r^2} \end{gather}$$

由于电荷在球面上分布，内部无电荷，所以 $r<R$ 时 $E=0$。

---

带电量为q的球体半径为R，电荷体密度为$\rho$。求某点处E

$r>R$ 时，同上；

$r<R$ 时，$E\not=0$。只有$\le r$部分的电荷有作用：

$$\begin{gather} E\cdot 4\pi r^2=\frac1 {\varepsilon_0}\int_0^r\rho\mathrm dV=\frac1{\varepsilon_0}\rho\frac43\pi r^3\\ \therefore E=\frac{\rho}{3\varepsilon_0}r \end{gather}$$

---

无限大均匀带电板上电荷面密度为$\rho$，求E分布

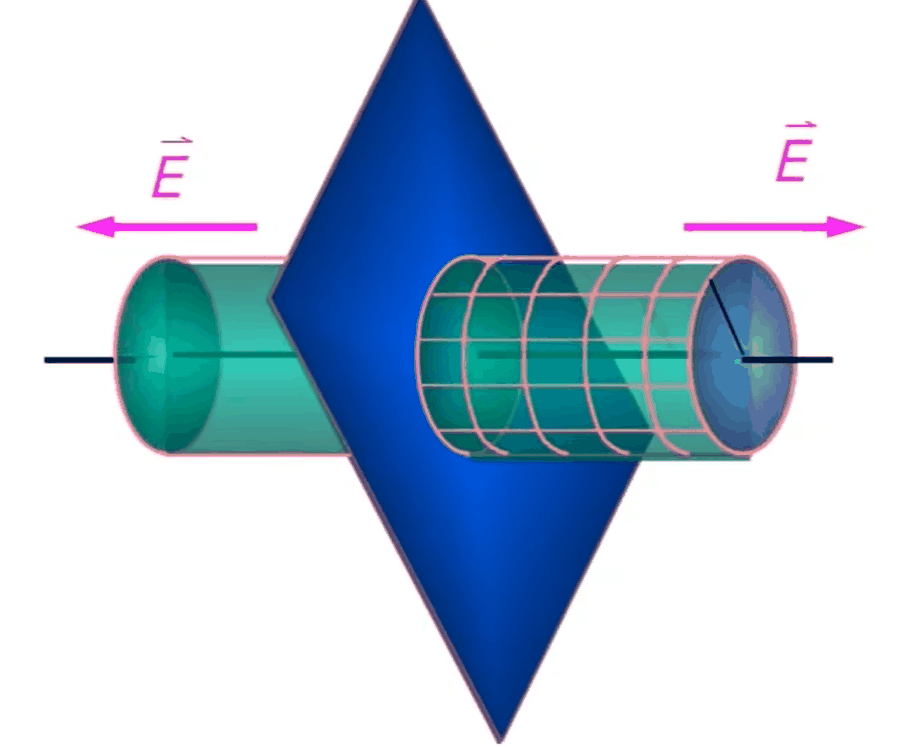
如上图选取高斯面

$$\begin{gather} \phi_e=\int_{侧面}\vec E\cdot \mathrm d\vec S+\int_{左底}\vec E\cdot \mathrm d\vec S+\int_{右底}\vec E\cdot \mathrm d\vec S\\ =0+ES+ES=2ES\\ 2ES=\frac1{\varepsilon_0}\sigma S\\ E=\frac{\sigma}{2\varepsilon_0} \end{gather}$$

电势

单位正电荷从该点移动到势能零点过程中，电场力做的功。

$$u_a=u_{a0}=\int_a^{0}\vec E\cdot \mathrm d\vec l$$

点电荷的电势

$$\begin{gather} u_a=\int_a^\infty \vec E\cdot \mathrm d\vec l=\frac{q}{4\pi \varepsilon_0}\int_r^\infty\frac{\mathrm dr}{r^2}=\frac{q}{4\pi \varepsilon_0 r} \end{gather}$$

电容

$$\begin{gather} E=\frac Ud\\ C=\frac QU=\frac{\varepsilon_0\varepsilon_rS}{d}\\ W=\frac12CU^2\\ \end{gather}$$

例：将平行电容板充电后与电源断开，将其$d$拉大，问电势差$U_{12}$、电场强度$E$、电场能量$W$的变化

电源断开，所以$Q$不变

$$\begin{gather} C\downarrow\propto\frac{S}{d\uparrow}\\ U\uparrow=\frac{Q}{C\downarrow}\\ E=\frac{U\uparrow}{d\uparrow}=\frac{Q}{C\downarrow d\uparrow}\propto \frac{Q}{S}\\ W\uparrow=\frac12 C\downarrow U^2\uparrow\propto U\uparrow \end{gather}$$

恒定磁场

电流强度

$$\begin{gather} I=\frac{\mathrm dq}{\mathrm dt}=\frac Qt \end{gather}$$

是一个标量，但是为了电路处理方便，规定正电荷移动方向是电流方向。

磁感应强度

小磁针在磁场中，北极N的指向为 $\vec B$ 的方向。

毕萨定律

大小

$$\begin{gather} \mathrm d\vec B=\frac{\mu_0}{4\pi}\frac{I\mathrm d\vec l\times \vec r_0}{r^2} \end{gather}$$

方向：右手螺旋定则，从 $I\mathrm d\vec l$ 握到 $\vec r_0$，也可以大拇指顺电流手握导线。

---

载流直导线的磁场

求距离载流直导线为a处的一点P的磁感应强度$\vec B$

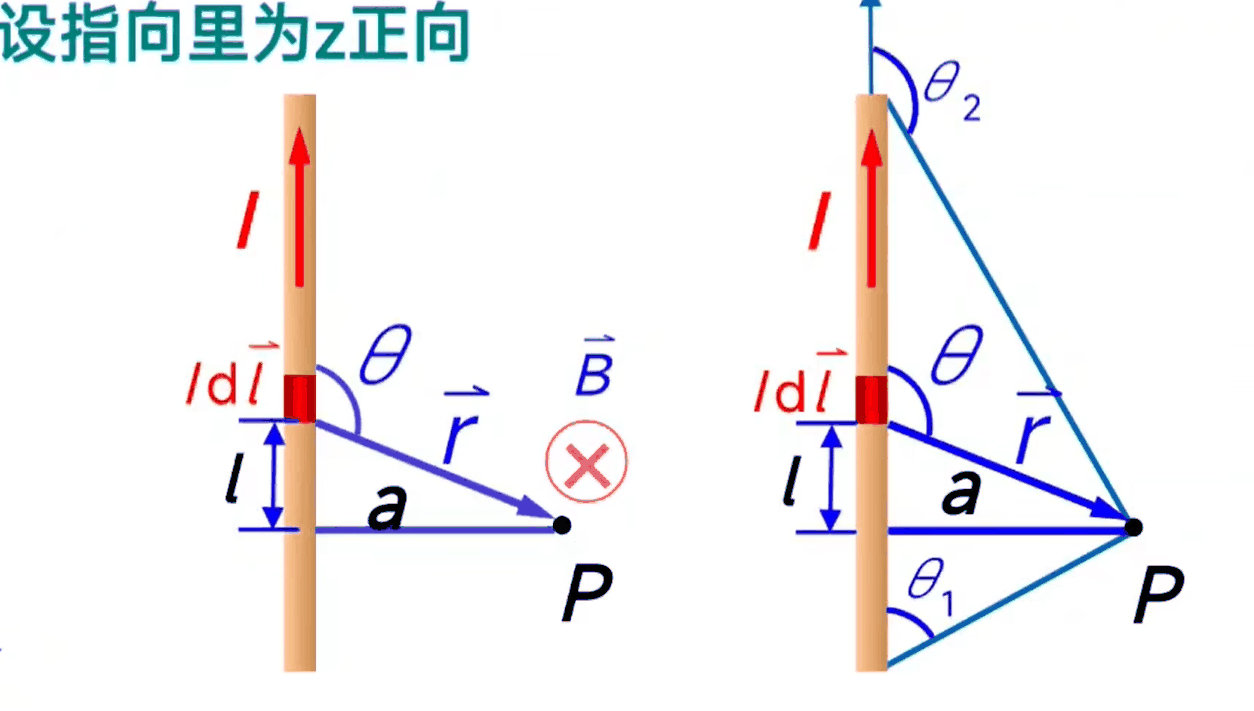$$\begin{gather} \mathrm dB=\frac{\mu_0}{4\pi} \frac{I\mathrm dl\sin\theta}{r^2}\\ r=a\csc\theta\\ l=a\cot(\pi-\theta)=-a\cot\theta\\ \mathrm dl=a\csc^2\theta\mathrm d\theta\\ B_z=B=\int\frac{\mu_0}{4\pi} \frac{I\mathrm dl\sin\theta}{r^2}=\frac{\mu_0I}{4\pi a}(\cos\theta_1-\cos\theta_2) \end{gather}$$

如果把 $\theta_2$ 换成三角形的内角更好记一点，就是 $\frac{\mu_0I}{4\pi a}(\cos\theta_1+\cos\theta_2)$ 了

无限长直导线的磁场

$\theta_1\to 0,\theta_2\to \pi$

$$\begin{gather} B=\frac{\mu_0I}{2\pi a} \end{gather}$$

任意形状直导线

分成多段直导线，矢量叠加

---

载流圆线圈的磁场

半径 $R$ 的载流 $I$ 圆线圈上一点 $P$ 的磁感应强度

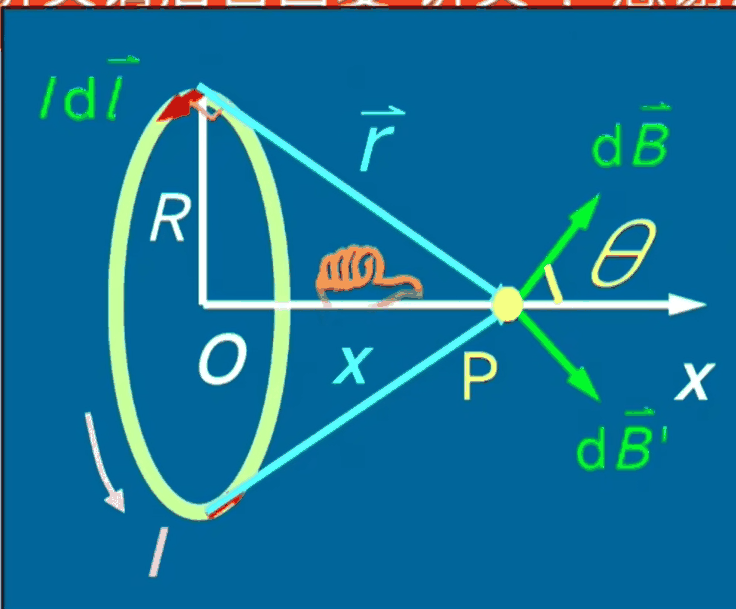$$\begin{gather} \mathrm dB=\frac{\mu_0I\mathrm dl}{4\pi r^2}=\frac{\mu_0I\mathrm dl}{4\pi(R^2+x^2)}\\ B_\perp=0\\ B=\int\mathrm dB\cos\theta=\int\frac{\mu_0}{4\pi}\frac{I\mathrm dl}{r^2}\cos\theta\\ =\int\frac{\mu_0}{4\pi}\frac{I\mathrm dl}{r^2}\frac Rr=\frac{\mu_0IR}{4\pi(R^2+x^2)^\frac 32}2\pi R\\ =\frac{\mu_0IR^2}{2(R^2+x^2)^\frac32} \end{gather}$$

载流圆线圈圆心处

$x=0$

$$\begin{gather} B=\frac{\mu_0I}{2R} \end{gather}$$

一段载流圆弧圆心处

圆弧所对的圆心角为$\phi$

$$\begin{gather} B=\frac{\mu_0I}{2R}\cdot\frac{\phi}{2\pi} \end{gather}$$

---

绕轴旋转的带电圆盘轴线上的磁场

带电 $q$ 的圆盘以角速度 $\omega$ 旋转，求轴线上 $x$ 处磁场

$$\begin{gather} \sigma=\frac{q}{\pi R^2}\\ \mathrm dq=\sigma\cdot2\pi r\mathrm dr\\ \mathrm dI=\frac{\mathrm dq}{\mathrm dt}=\frac{\sigma\cdot2\pi r\mathrm dr}{2\pi\omega}=\omega \sigma r\mathrm dr\\ \mathrm dB=\frac{\mu_0r^2\mathrm dI}{2(r^2+x^2)^\frac32}\\ =\frac{\mu_0\sigma\omega r^3\mathrm dr}{2(r^2+x^2)^\frac32}\\ B=\frac{\mu_0\sigma\omega}2[\frac{R^2+2x^2}{\sqrt{x^2+R^2}}-2x] \end{gather}$$

磁感线

1. 无头无尾闭合曲线
2. 与电流套连，服从右手螺旋
3. 不相交

磁通量：通过某个面元的磁感线条数

规定磁感线穿入$\phi_m<0$，穿出$\phi_m>0$

磁感线的高斯定理

由于磁感线闭合，所以

$$\begin{gather} \phi_m=\oint_S\vec B\cdot\mathrm d\vec S=0 \end{gather}$$

磁场的安培环路定理

电场中，绕一圈回来，电场力不做功；

磁场中则与环路包围着的电流有关：

$$\begin{gather} \oint_L\vec B\cdot \mathrm d\vec l=\mu_0I \end{gather}$$

要求：

1. 环路 $L$ 与 $B$ 同向。如果 $L$ 反向，则为$-\mu_0I$。
2. 对于一段导线不成立。只适用于闭合导线

安培定理

$$\begin{gather} \mathrm dF=I\mathrm d\vec l\times \vec B \end{gather}$$

注意方向，$\vec l\times \vec B$

均匀磁场中形状任意的导线受力

电流强度为 $I$

等价于起点与终点连线的导线的受力 $F=BIL’$

平行无限长直导线之间的相互作用力

$$\begin{gather} B_1=\frac{\mu_0I_1}{2\pi a}\\ (单位长度受到的作用力)f_{12}=I_{2}B_1=\frac{\mu_0I_1I_2}{2\pi a} \end{gather}$$

电流同向相吸，异向排斥。

洛伦兹力

安培力是大量粒子洛伦兹力的叠加

对一个电荷研究

$$\begin{gather} \vec f_m=q\vec v\times \vec B \end{gather}$$

代入$I=envS\Rightarrow v=\frac{I}{enS}$

$$\begin{gather} f_m=qvB=\frac{BI}{nS} \end{gather}$$

做圆周运动

$$\begin{gather} qvB\sin\frac\pi2=m\frac{v^2}{R}\\ R=\frac{mv}{qB}\\ T=\frac{2\pi R}{v}=\frac{2\pi m}{qB}\\ f=\frac{qB}{2\pi m} \end{gather}$$

电磁感应

电磁感应定律

$$\begin{gather} \phi=\int\vec B\cdot\mathrm d\vec S\\ \varepsilon=-\frac{\mathrm d\phi}{\mathrm dt} \end{gather}$$

负号表示方向，阻碍磁通量的变化（楞次定律）

若回路中有电阻 $R$

$$\begin{gather} I_i=\frac \varepsilon R=-\frac{\mathrm d\phi}{R\mathrm dt}=\frac{\mathrm dq_i}{\mathrm dt}\\ 感应电荷q_i=\int_{t_1}^{t_2}-\frac1R\mathrm d\phi=\frac{\phi_1-\phi_2}R \end{gather}$$

例：大小同心圆环，$r_1\ll r_2$，大线圈有电流$I$，当小线圈环绕其直径以 $\omega$ 转动时，求小圆环中的感应电动势

大圆环在圆心处的磁场

$$\begin{gather} B=\frac{\mu_0I}{2r_2} \end{gather}$$

通过小线圈的磁通量

$$\begin{gather} \phi=\vec B\cdot \vec S=\frac{\mu_0I}{2r_2}\pi r_1^2cos\omega t \end{gather}$$

所以感应电动势

$$\begin{gather} \varepsilon=-\frac{\mathrm d\phi}{\mathrm dt}=\frac{\mu_0I\pi r_1^2\omega}{2r_2}\sin\omega t \end{gather}$$

---

例：无限载流长直导线的磁场中，一运动导体线框以速度 $v$ 作远离导线运动，且始终与长直导线共面。求线框的感应电动势

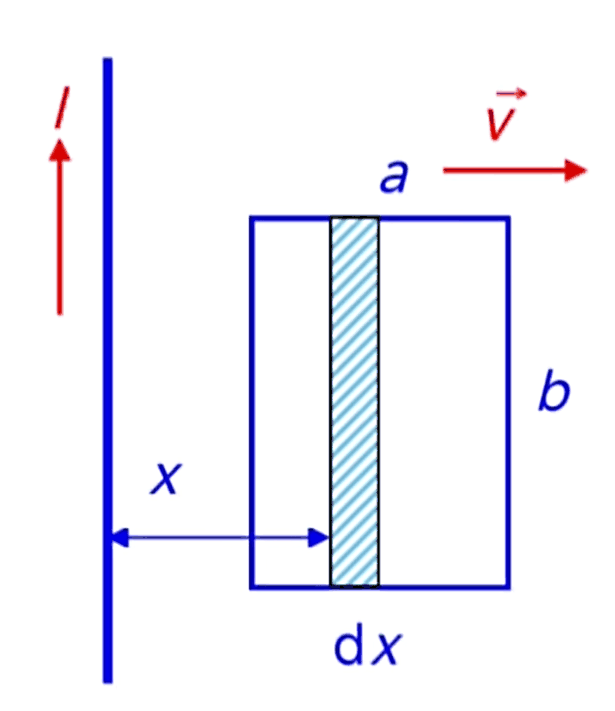$$\begin{gather} \mathrm d\phi=B\mathrm dS=\frac{\mu_0I}{2\pi x}b\mathrm dx\\ \phi=\int_L^{L+a}\mathrm d\phi\\ =\frac{\mu_0Ib}{2\pi}\int_L^{L+a}\frac{\mathrm dx}x\\ =\frac{\mu_0Ib}{2\pi}\ln\frac{L+a}{L}\\ L=vt,\mathrm dL=v\mathrm dt\\ \varepsilon=-\frac{\mathrm d\phi}{\mathrm dt}=-\frac{\mu_0Ib}{2\pi}[\frac{\frac{\mathrm dL}{\mathrm dt}}{L+a}-\frac {\frac{\mathrm dL}{\mathrm dt}}{l}]\\ =\frac{\mu_0Iabv}{2\pi L(L+a)} \end{gather}$$

感应电动势

两种感应机制

1. 动生电动势：磁场不变，回路运动切割磁感线
2. 感生：回路静止，磁场随时间变化

动生电动势

其原理是电子受洛伦兹力

$$\begin{gather} \vec f=-e(\vec v\times \vec B) \end{gather}$$

即非静电力$\vec F_k$

$$\begin{gather} \vec E_k=\frac{\vec F_k}{-e}=\vec v\times \vec B\\ \varepsilon_i=\int_-^+\vec E_k\cdot \mathrm d\vec l=\int_-^+(\vec v\times \vec B)\cdot \mathrm d\vec l \end{gather}$$

例：匀强磁场 $B$ 中，长为 $R$ 的铜棒绕其一端 $O$ 以角速度 $\omega$ 在垂直于 $B$ 的平面内转动，求棒上的电动势

方法一（动生电动势）

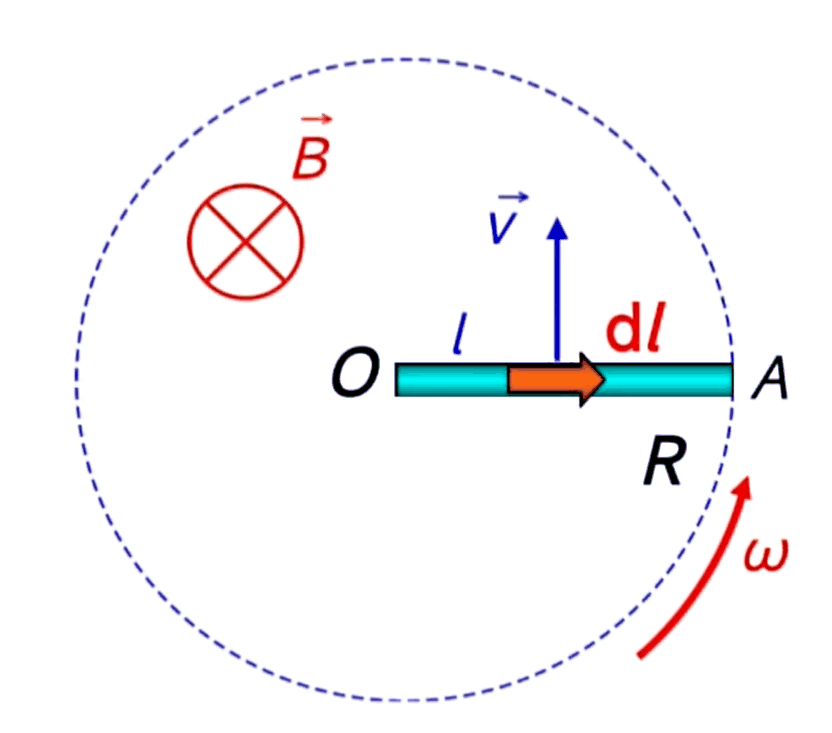$$\begin{gather} \varepsilon_i=\int_O^A(v\times B)\cdot \mathrm dl\\ =\int_0^R l\omega B\mathrm dl\\ =\frac{BR^2}{2}\omega \end{gather}$$

用右手螺旋法则判断方向为$A\to O$。

方法二（法拉第电磁感应定律）

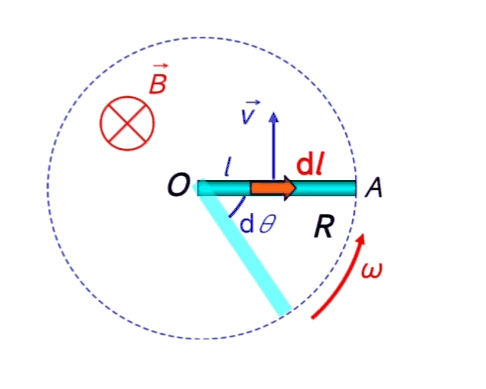
在$\mathrm dt$的时间内导体切割磁感线，切割了一个扇形

$$\begin{gather} \mathrm d\phi=B\cdot\frac12 R^2\mathrm d\theta\\ \varepsilon_i=\frac{\mathrm d\phi}{\mathrm dt}=\frac12 BR^2\frac{\mathrm d\theta}{\mathrm dt}=\frac12BR^2\omega \end{gather}$$

由楞次定律，电流应当产生一个向外的点磁场来阻止其增大。为了在图中扇形区域产生“点”场，电流$O\to A$

感生电动势

$\varepsilon_i=\int_a^b\vec E_v\cdot \mathrm d\vec l$，其中$\vec E_v$是感生电场

感生电场与变化磁场之间的关系

$$\begin{gather} \oint_L\vec E_v\cdot \mathrm d\vec l=-\int_S\frac{\partial \vec B}{\partial t}\cdot \mathrm d\vec S \end{gather}$$

即，感生电动势=感生电场对于长度的积分=负的(磁场关于时间的变化量)对于平面的积分。