CF1988D The Omnipotent Monster Killer

发表于 阅读次数： 本文字数： 757 阅读时长 ≈ 3 分钟

CF1988D The Omnipotent Monster Killer

Problem

怪物们在一棵有 \(n\) 个顶点的树上，编号为 \(i(1\le i\le n)\) 的怪物位于编号为 \(i\) 的顶点上，攻击力为 \(a_i\) 。你需要与怪物战斗 \(10^{100}\) 个回合。在每个回合中，会依次发生以下两步：

  1. 所有活着的怪物攻击你。你的生命值会按照所有活体怪物攻击点的总和减少。
  2. 您选择一些（可以选全部，也可以不选）怪物并杀死它们。被杀死的怪物将不会再进行攻击。

限制条件：在一个回合内不能杀死相邻的两只怪物。

如果您以最佳选择方式攻击的怪物，那么在所有回合后，您的健康值减少的最小值是多少？

\(1\le t\le 10^4,1\le n\le 3\cdot 10^5,1\le a_i \le 10^{12},\sum n\le 3\cdot 10^5\)

Solution

这是一道再经典不过的树形DP了。太惭愧了。

每个节点的贡献可以表示为 \(w_i\cdot a_i\) 的形式，其中 \(w_i\) 表示怪物 \(i\) 是第 \(w_i\) 次被杀死的。可以证明 \(w_i\) 不会超过 \(\log_2(n)\) 。

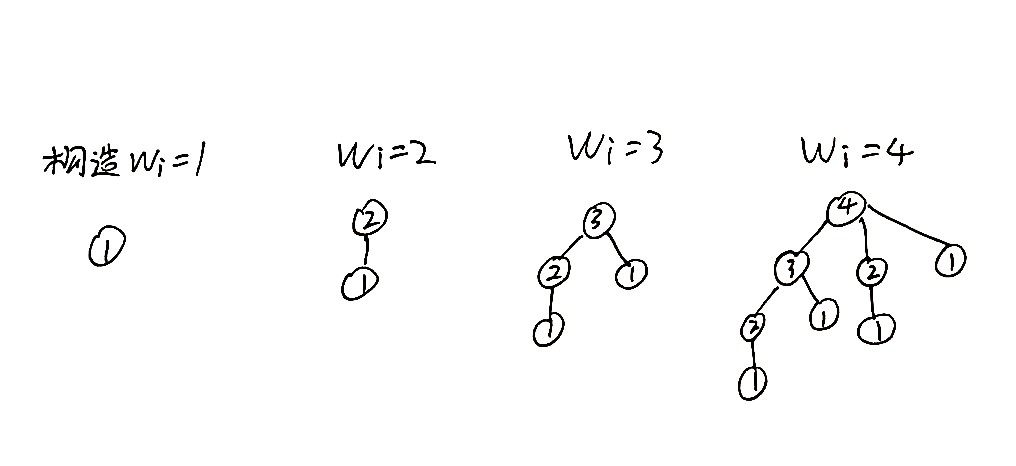
图：Taibo

上图中，欲构造出 \(w_i=x\) 的点，需要将该点连接上 \(w=1,2,\dots,x-1\) 的节点。设构造出 \(\max w_i=n\) 的树至少需要 \(tot_n\)​ 个节点，则存在 \[ \begin{gather} tot_n= \begin{cases} & 1 & n=1\\ & \sum_{i=1}^{n-1}tot_i +1 & n\ge 2 \end{cases} \end{gather} \] 即得 \(tot_n=2^n\) 。也就是说对于一张 \(n\) 个节点的图，其至多需要 \(\log_2(n)\) 次选择就可以将所有怪物杀死。

下面开始dp。设 \(dp_{x,k}\) 表示若第 \(k\) 次杀死怪物 \(x\) ， \(x\) 子树内的怪物至少会产生多少点伤害。

\(dp_{x,k}\) 由两部分组成：

  • 在第 \(k\) 次杀死怪物 \(x\) 之前，怪物 \(x\) 会产生 \(k\cdot a_x\) 点伤害。
  • \(x\) 的子树内的怪物（除了 \(x\) 本身）产生的伤害。

\[ \begin{gather} dp_{x,k}=k\cdot a_x + \sum_{y\in u(x)}\min_{j\not =k} dp_{y,j} \end{gather} \]

其中 \(u(x)\) 表示点 \(x\)​ 的儿子节点。

最后答案为 \(\min dp_{root,k}\)

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
#define N 300010

int n;
int head[N],nxt[N*2],ver[N*2],cnt;
void insert(int x,int y)
{
    nxt[++cnt]=head[x];
    head[x]=cnt;
    ver[cnt]=y;
}


LL a[N];

#define K 25
#define inf (1ll<<62)
LL dp[N][K+5];

void dfs(int x,int f)
{
    for(int i=1;i<=K;i++)
    {
        dp[x][i]=a[x]*i;
    }
    
    for(int i=head[x];i;i=nxt[i])
    {
        int y=ver[i];
        if(y==f) continue;
        dfs(y,x);
        for(int j=1;j<=K;j++)//点x将被第j次选
        {
            LL mn=inf;
            for(int k=1;k<=K;k++)//相邻点y将被第k次选
            {
                if(j!=k)
                {
                    mn=min(mn,dp[y][k]);
                }
            }
            dp[x][j]+=mn;
        }
    }
}



int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cout.precision(10);
    int t=1;
    cin>>t;
    while(t--)
    {
        cin>>n;
        for(int i=1;i<=n;i++)
        {
            cin>>a[i];
        }
        for(int i=1;i<n;i++)
        {
            int x,y;cin>>x>>y;
            insert(x,y);
            insert(y,x);
        }
        
        dfs(1,0);
        
        LL ans=inf;
        for(int i=1;i<=K;i++)
        {
            ans=min(ans,dp[1][i]);
        }
        
        cout<<ans<<endl;
        
        
        for(int i=1;i<=cnt;i++)
        {
            head[i]=nxt[i]=ver[i]=0;
        }
        cnt=0;
    }
    return 0;
}