第五次优秀论文研读报告——2023多波束测线问题

发表于 更新于 阅读次数： 本文字数： 2.9k 阅读时长 ≈ 11 分钟

2023多波束测线问题

问题一模型建立与求解

第一问是一个平面几何题，两篇优秀论文方法和答案都差不多，就不分开讲述了。当海底面为一个与水平面夹角为α的坡面，且测线方向与水平面平行时，那么每条测线与海底面的交线均为海底面的等高线，结合解析几何相关知识，可以建立计算多波束测深的覆盖宽度模型以及计算相邻条带之间重叠率的模型。

alt

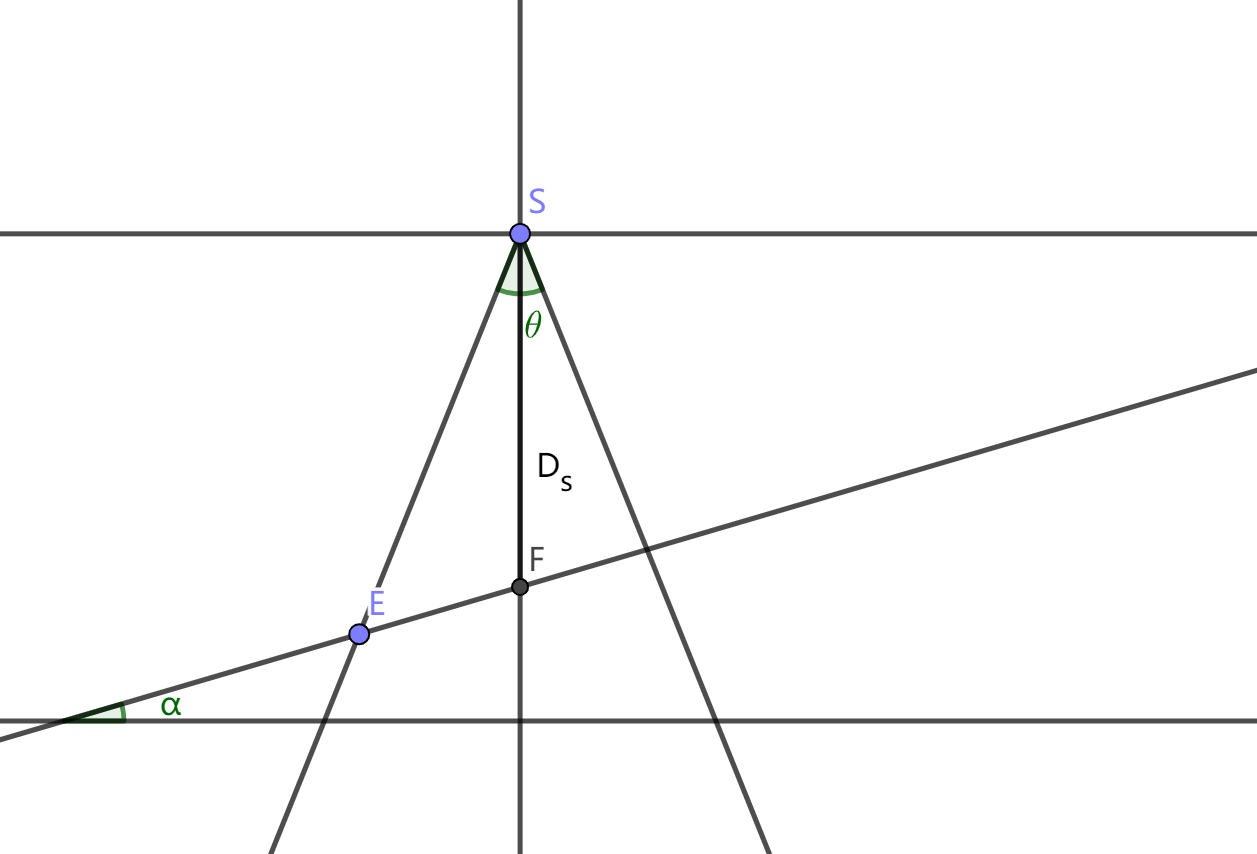
确定已知量：\(\alpha,\theta,D_{s0},d\)

向右移动\(d\)导致的深度变化： \[ \begin{align} D_s=D_{s0}-d\tan\alpha \end{align} \] 确定角度时，利用正弦定理计算多波束扫描的左右宽度： \[ \begin{align} EF=W_1=D_s\frac{\sin\frac{\theta}{2}}{\sin(90-\frac\theta2-\alpha)}\\ FG=W_2=D_s\frac{\sin\frac{\theta}{2}}{\sin(90-\frac\theta2+\alpha)} \end{align} \] 对于重合率，题目给的是\(\eta=1-\frac dW\)，但是这个公式仅适用于海底是平坦的情况。当海底倾斜时，需要重新推导公式。

alt

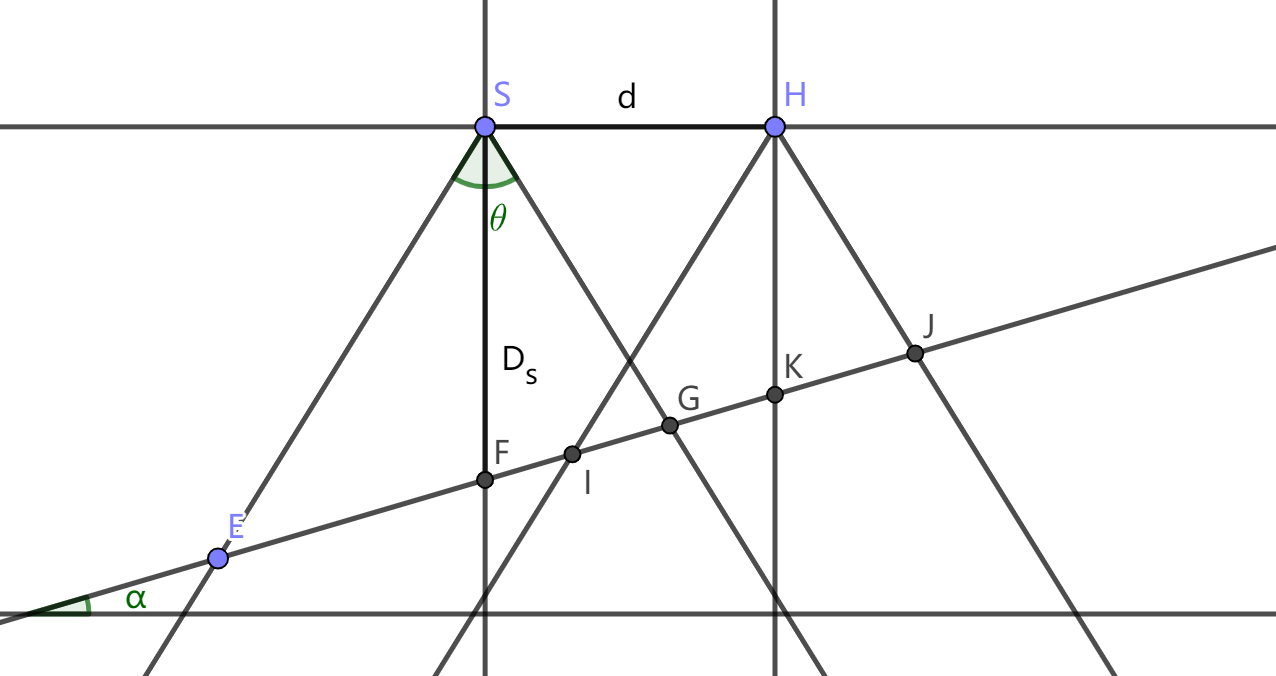
图中，从S和H发出了两平行多波束的重合部分为\(IG\)，而H射出的宽度\(IJ\)记作W，则有： \[ \begin{align} IG&=FG+IK-FK\\ &=W_2(D_s)+W_1(D_h)-\frac{d}{\cos\alpha}\\ &=D_s\frac{\sin\frac{\theta}{2}}{\sin(90-\frac\theta2+\alpha)}+(D_s-d\tan\alpha)\frac{\sin\frac{\theta}{2}}{\sin(90-\frac\theta2-\alpha)}-\frac{d}{\cos\alpha} \end{align} \]

\[ \begin{align} W=W_1(D_h)+W_2(D_h) \end{align} \]

\[ \begin{align} \eta=\frac{IG}{W} \end{align} \]

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
/**************************************************************
 * Problem: 
 * Author: Vanilla_chan
 * Date: 
 * E-Mail: heshaohong2015@outlook.com
 **************************************************************/
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<string>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#include<limits.h>
#define IL inline
#define re register
#define LL long long
#define ULL unsigned long long
#ifdef TH
#define debug printf("Now is %d\n",__LINE__);
#else
#define debug
#endif
#ifdef ONLINE_JUDGE
char buf[1<<23],* p1=buf,* p2=buf,obuf[1<<23],* O=obuf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
#endif
using namespace std;


double D0=70,alpha=1.5,theta=120;
int d=200;
double hudu(double angle)
{
    return angle/180*acos(-1);
}
double D(double x)
{
    return D0-x*tan(hudu(alpha));
}

double W1(double x)
{
    return D(x)*sin(hudu(theta/2))/sin(hudu(90-theta/2-alpha));
}
double W2(double x)
{
    return D(x)*sin(hudu(theta/2))/sin(hudu(90-theta/2+alpha));
}



int main()
{
    for(int x=-800;x<=800;x+=d)
    {
        cout<<D(x)<<"\t"<<W1(x)+W2(x)<<"\t"<<(W1(x)+W2(x-d)-d*cos(hudu(alpha)))/(W1(x)+W2(x))<<endl;
    }
    return 0;
}

结果如下表：

\(d\) -800 -600 -400 -200 0 200 400 600 800
\(D_s\) 90.9487 85.7116 80.4744 75.2372 70 64.7628 59.5256 54.2884 49.0513
\(W\) 315.813 297.628 279.442 261.256 243.07 224.884 206.699 188.513 170.327
\(\eta\) 0.394418 0.357415 0.315596 0.267956 0.213186 0.149559 0.0747355 -0.0145244 -0.122845

两篇优秀论文的结果都一致。虽然题目中给出了重叠率的计算公式为\(\eta=1-\frac dW\)，但是他们都避开了这个陷阱。

问题二模型建立与求解

问题二则将问题一拓展到了一个具有倾斜平面的海底，该海底倾斜角度为\(\alpha\)。

alt

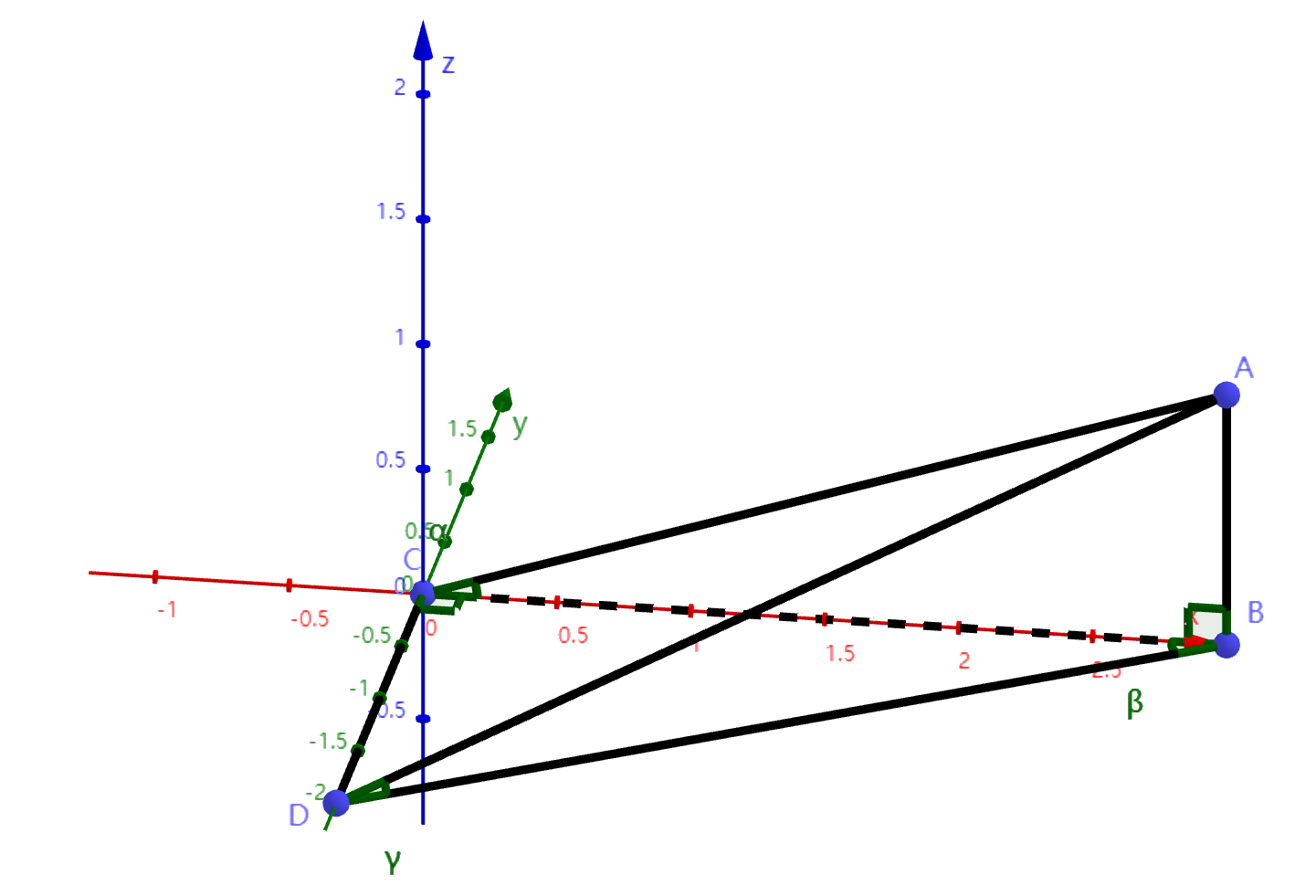
图中AC是海底平面ACD的法向量在该平面上的投影，\(\tan\alpha=\frac{AB}{BC}\)

\(\beta\)是船行驶平面ABD与海底平面的法向量投影AC的夹角，也是ABD与BC的夹角，\(\cos\beta=\frac{BC}{BD}\)

而我们希望得到的“船向前开时海底上升的角度\(\gamma_1\)”满足\(\tan \gamma=\frac{AB}{BD}=\tan\alpha\cos\beta\)。这个角度将决定船的行驶距离与海底深度之间的关系。

alt

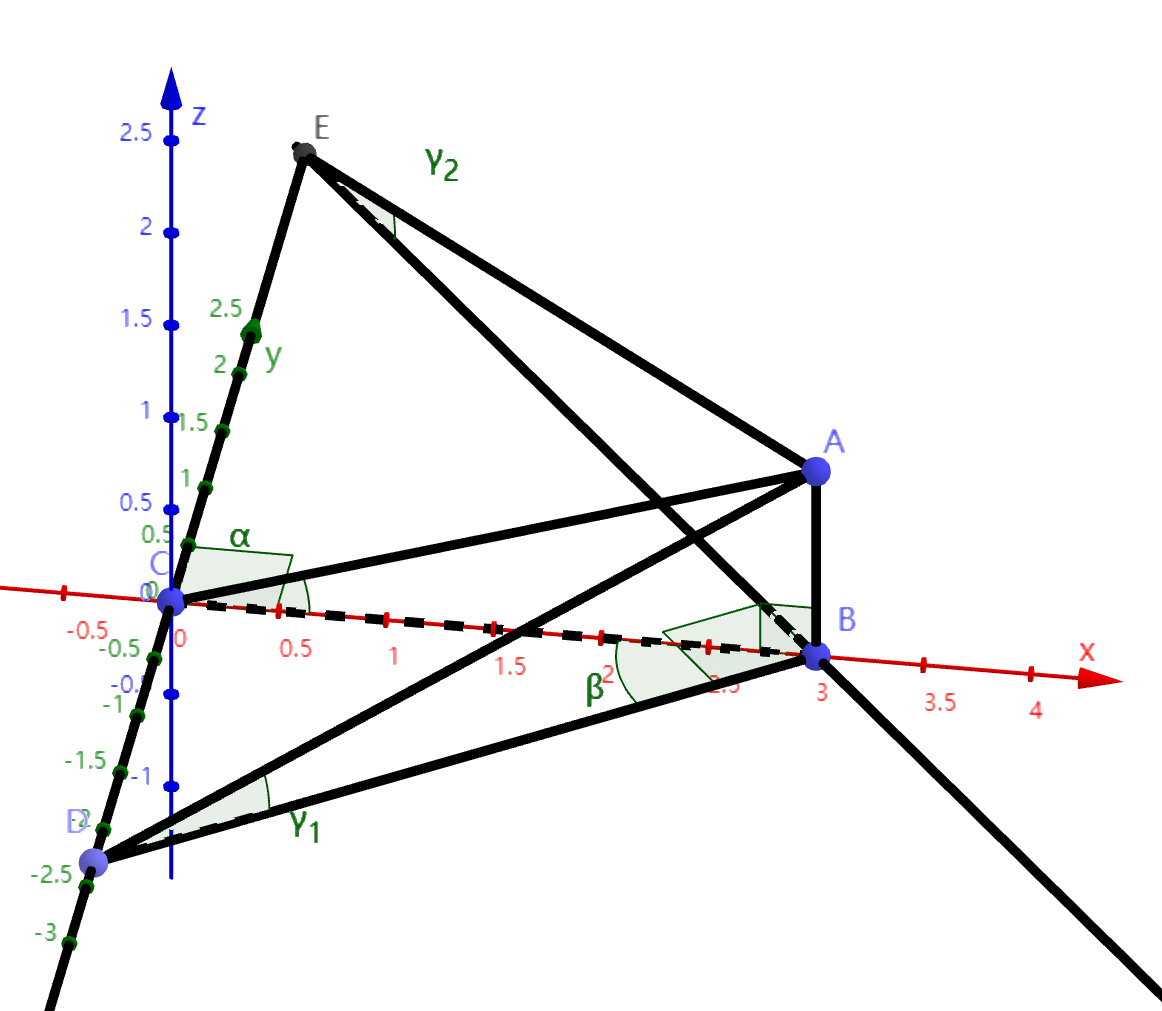
然后我们还需要计算“船以\(\beta\)的旋转角向前行驶时，某时某刻，其扫描平面下，海底的倾斜角度”。

如上图，当船位于A点的正上方，且行驶平面为ABD时，多波束仪器会在垂直于船行驶方向的平面内进行扫描，即ABE平面。此时，海底扫描的形状为AE，则需要求出AE的倾斜角\(\gamma_2\) \[ \begin{align} &\tan\gamma_2=\frac{AB}{BE}\\ &\cos(90^\circ-\beta)=\frac{BC}{BE}\\ &\tan\alpha=\frac{AB}{BC} \end{align} \] 则得到\(\tan\gamma_2=\tan\alpha\cos(90^\circ-\beta)\)

至此，我们得到了\(\gamma_1,\gamma_2\)。

船只所在位置的深度计算：\(D(\beta,L)=D(\beta,0)+L\times\tan\gamma_1\)

船只扫描宽度计算： \[ \begin{align} W_1(\beta,L)&=D(\beta,L)\frac{\sin\frac\theta2}{\sin(90^\circ-\frac{\theta}2-\gamma_2)}\\ W_2(\beta,L)&=D(\beta,L)\frac{\sin\frac\theta2}{\sin(90^\circ-\frac{\theta}2+\gamma_2)}\\ W&=W_1+W_2 \end{align} \] 最终得到了第二问完整模型。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
/**************************************************************
 * Problem: 
 * Author: Vanilla_chan
 * Date: 
 * E-Mail: heshaohong2015@outlook.com
 **************************************************************/
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<string>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#include<limits.h>
#define IL inline
#define re register
#define LL long long
#define ULL unsigned long long
#ifdef TH
#define debug printf("Now is %d\n",__LINE__);
#else
#define debug
#endif
#ifdef ONLINE_JUDGE
char buf[1<<23],* p1=buf,* p2=buf,obuf[1<<23],* O=obuf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
#endif
using namespace std;


double D0=120,alpha=1.5,theta=120;
double hudu(double angle)
{
    return angle/180*acos(-1);
}
double jiaodu(double angle)
{
    return angle/acos(-1)*180;
}

double gamma_1(double beta)
{
    return jiaodu(atan(tan(hudu(alpha))*cos(hudu(beta))));
}
double gamma_2(double beta)
{
    return jiaodu(atan(tan(hudu(alpha))*cos(hudu(90-beta))));
}
double D(double x,double beta)
{
    return D0+x*tan(hudu(gamma_1(beta)));
}
double W1(double x,double beta)
{
    return D(x,beta)*sin(hudu(theta/2))/sin(hudu(90-theta/2-gamma_2(beta)));
}
double W2(double x,double beta)
{
    return D(x,beta)*sin(hudu(theta/2))/sin(hudu(90-theta/2+gamma_2(beta)));
}
int main()
{
    for(double beta=0;beta<360;beta+=45)
    {
        for(double x=0;x<=2.1;x+=0.3)
        {
            cout<<W1(x*1852,beta)+W2(x*1852,beta)<<"\t";
        }
        cout<<endl;
    }
    return 0;
}

结果如下：

覆盖宽度 0 0.3 0.6 0.9 1.2 1.5 1.8 2.1
0 415.692 466.091 516.49 566.889 617.288 667.686 718.085 768.484
45 416.192 451.872 487.552 523.232 558.912 594.592 630.273 665.953
90 416.692 416.692 416.692 416.692 416.692 416.692 416.692 416.692
135 416.192 380.511 344.831 309.151 273.471 237.791 202.11 166.43
180 415.692 365.293 314.894 264.496 214.097 163.698 113.299 62.9002
225 416.192 380.511 344.831 309.151 273.471 237.791 202.11 166.43
270 416.692 416.692 416.692 416.692 416.692 416.692 416.692 416.692
315 416.192 451.872 487.552 523.232 558.912 594.592 630.273 665.953

论文中存在的问题

论文4开始想要对\(\beta\)进行锐角和钝角的分类讨论，并且只考虑了锐角的情况，所以接下来的很多角度计算都打了绝对值。但是之后模型建立时忘记考虑钝角的情况了，没有将绝对值去除。但是但是，最后答案表格是全部正确的。

以及模型建立时，错误的写成了\(D_{\beta s}=D_{\beta 0}-L\tan\gamma_1\)，正负号错误。

问题三模型建立与求解

问题三是在问题二的基础上，进行布线。论文3和4在这里出现了分歧。

论文4只做出了“仅考虑直线布线”的假设，还是对于船只行驶角度\(\beta\)进行了讨论与计算，所以花了很大的篇幅进行建模、综合模型、特殊情况判断，非常多的分类讨论，而且还考虑了船需要多开一点\(\omega_1,\omega_2\)才能完全覆盖整片海域。最后貌似只是把模型列出来，叙述了贪心求解方法，只列出了取\(\beta=90^\circ\)（包括代码中也缺少了），即船只沿着等深线行驶的情况。

论文3直接通过查阅资料《海洋多波束水深测量规程》要求规范，确定主测线一般按照平行于等深线走向布设。所以建模的时候直接选择了\(\beta=90^\circ\)。之后同样通过贪心的方法求解，但是还进一步的使用了模拟退火（在贪心求解的结果上进行微调）进行验证贪心得到的答案是最优的。这一步可以说更完备，也可以说是多余的吧……

问题四模型建立与求解

alt

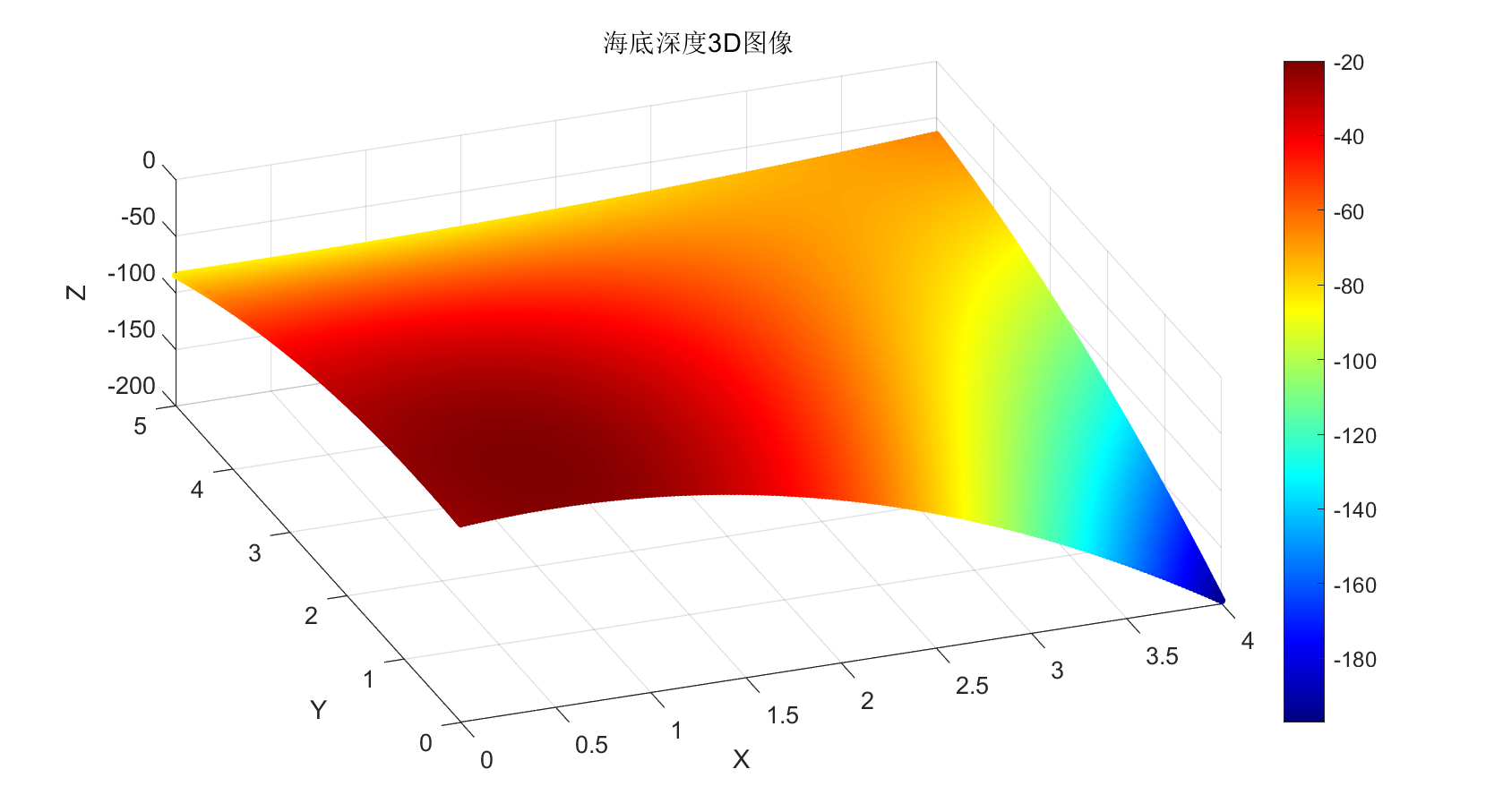
问题四分为两部分：一部分是对不规则的海底分割，用平面进行拟合；一部分是对拟合得到的结果使用问题三的方法求解。在这一问中有三个目标函数：

  1. 海域全覆盖
  2. 相邻条带之间的重叠率控制在20%以下
  3. 测线长度尽量短

论文4对曲面只分隔成了两块（使用平面\(\frac{x}4=\frac{y}5\)进行划分）然后使用最小二乘法进行拟合（分割数量太少了，效果不好）。

然后给出了一个收益计算公式，发现依然是沿着等高线开船时候收益最大，由此确定了船的行驶方向。

对于三个目标，论文4选择控制测线总长度最小为主要目标，其余为次要目标，依然使用贪心的铺设方法。

最后的结果没看懂。

论文4对等高线进行分析，然后手动的划分了很多区域。

alt

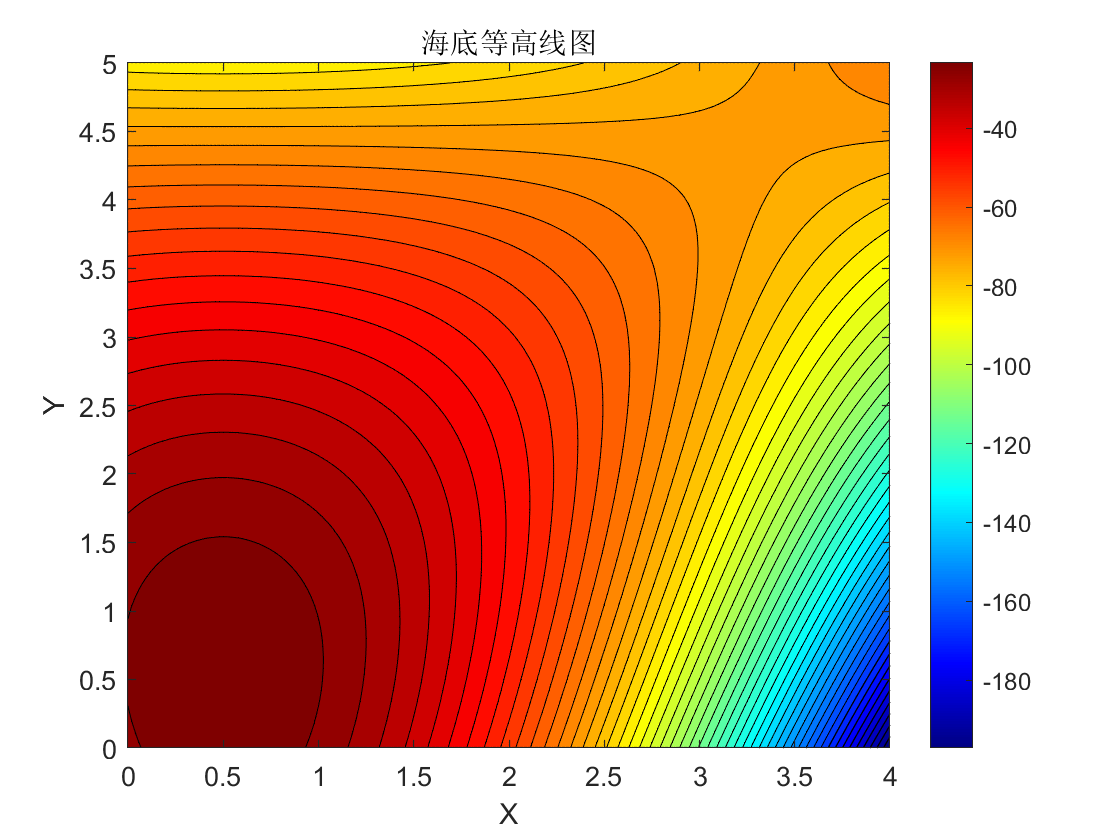
然后对于每个区域，为了使用平面方程\(z=Ax+By+C\)进行拟合，选择了最小二乘法，但是求解的时候并不是直接回归，而是使用粒子群算法这种随机算法。对于拟合效果不好的区域，进行进一步的划分。

为什么不用线性回归？这二元线性回归出来的结果不是好好的嘛：

alt

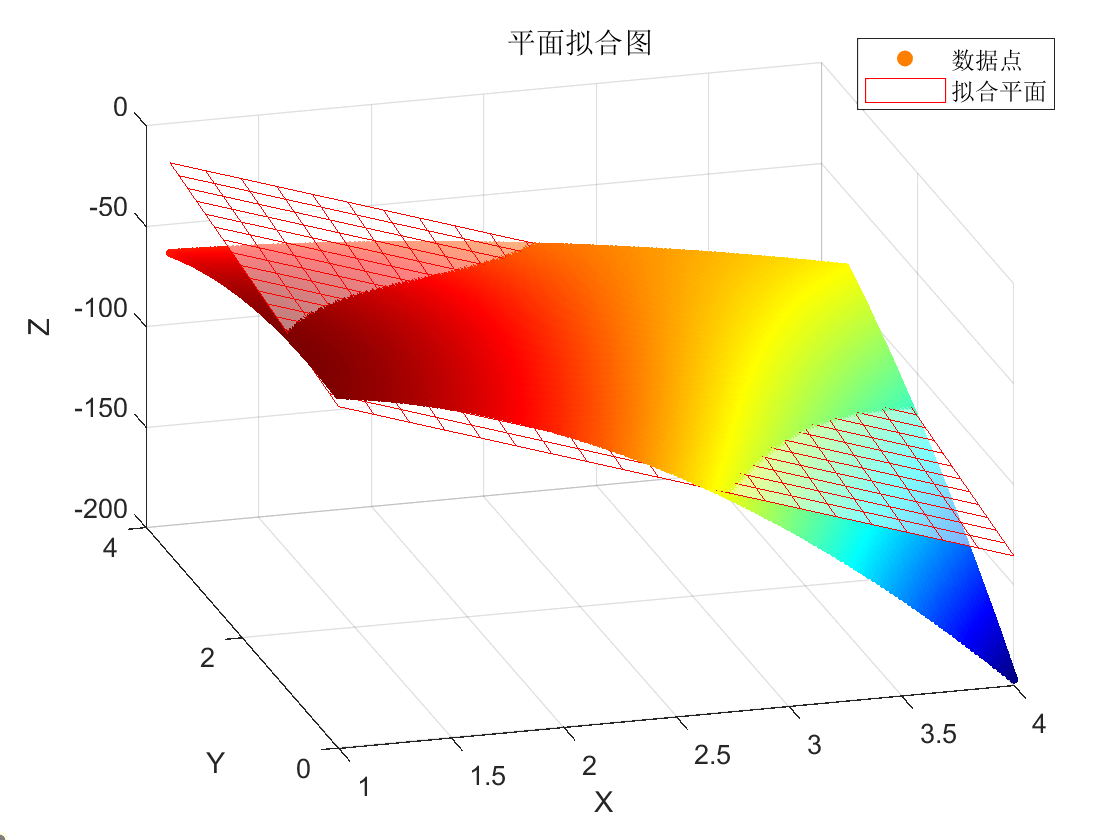
在大会上的解释是这样的：

如果使用了最小二乘法回归，得到的平面拟合效果确实好，但是下一步铺线的结果不一定好。所以这里用了一点小阴招，故意用粒子群算法随机出一些不那么好（指拟合效果不那么完美）的解，然后用这个解去做接下来一步的铺线，这样铺出来的效果相会于”完美拟合得到的平面的铺线“相比，漏测率和重叠率会更低。

所以说，更加准确的做法应该是修改平面拟合的目标函数，换成最小化下一步的漏测率和重叠率，合为一个模型来做。

绘图和分隔代码

论文3的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
table=readtable("附件.xlsx");
table=table(:,2:end);
data=table2array(table(2:end,2:end));

%% 统计数据
X=[];
Y=[];
Z=[];
for j=2:height(table)
    y=table2array(table(j,1));
    for i=2:width(table)
        x=table2array(table(1,i));
        z=table2array(table(j,i));
        X=[X,x];
        Y=[Y,y];
        Z=[Z,-z];
    end
end

%% 画图
figure;
scatter3(X, Y, Z, 10, Z, 'filled');
colorbar;
xlabel('X');
ylabel('Y');
zlabel('Z');
title('海底深度3D图像');
colormap(jet);
clim([min(Z), max(Z)]);

%% 等高线图
xlin = linspace(min(X), max(X), 201);
ylin = linspace(min(Y), max(Y), 251);
[Xgrid, Ygrid] = meshgrid(xlin, ylin);
Zgrid=-data;
figure;
contourf(Xgrid, Ygrid, Zgrid, 50);
colorbar;
xlabel('X');
ylabel('Y');
title('海底等高线图');
colormap(jet);


%% 划分
% 以区域I为例
% x=0~2，y=3.5~5
% [x_min, x_max, y_min, y_max] = deal(0, 2, 3.5, 5); % I
% [x_min, x_max, y_min, y_max] = deal(2, 4, 0, 3.5); % II

% [x_min, x_max, y_min, y_max] = deal(0, 1, 0, 3.5); % III
% [x_min, x_max, y_min, y_max] = deal(0, 1, 0, 0.5); % III'
% [x_min, x_max, y_min, y_max] = deal(0, 1, 0.5, 3.5); % V

% [x_min, x_max, y_min, y_max] = deal(1, 4, 0, 3.5); % IV
% [x_min, x_max, y_min, y_max] = deal(1, 2, 0, 3.5); % IV'
% [x_min, x_max, y_min, y_max] = deal(2, 4, 0, 3.5); % VI
indices = X >= x_min & X <= x_max & Y >= y_min & Y <= y_max;
X_region = X(indices);
Y_region = Y(indices);
Z_region = Z(indices);
Xb = [X_region; Y_region; ones(size(X_region))];
[b, bint, r, rint, stats] = regress(Z_region', Xb');

A = b(1);
B = b(2);
C = b(3);
disp('拟合系数 (A, B, C):');
disp(b');
disp('R-squared:');
disp(stats(1)); %R²
figure;
scatter3(X_region, Y_region, Z_region,10,Z_region, 'filled');
colormap(jet);
clim([min(Z_region), max(Z_region)]);
hold on;


[xGrid, yGrid] = meshgrid(linspace(x_min, x_max, 20), linspace(y_min, y_max, 20));
zGrid = A * xGrid + B * yGrid + C;
mesh(xGrid, yGrid, zGrid, 'EdgeColor', 'red', 'FaceAlpha', 0.5);
xlabel('X');
ylabel('Y');
zlabel('Z');
title('平面拟合图');
legend('数据点', '拟合平面');