代码手的自我修养

发表于 更新于 分类于 阅读次数： 本文字数： 11k 阅读时长 ≈ 42 分钟
本文包含了数据处理、常用函数介绍、算法实现、绘图等模块，最后提供了一些完整实例。

代码手的自我修养

数据处理

图片的读取与处理

读取图片

1
image = imread("图片文件路径");

imread() 根据图片文件路径读取图片，函数返回值为一个 \(3\times X\times Y\) 的uint8矩阵。

彩图转灰度图像

1
gray_image = rgb2gray(image);

rgb2gray() 转为灰度图像，函数返回值为 \(X\times Y\) 的uint8矩阵。

二值化

1
2
bw_image = gray_image < 85; % 二值化处理，阈值根据实际情况调整
bw2_image = imbinarize(gray_image); % 局部自适应二值化

得到了 \(X\times Y\) 的logical矩阵。

阈值二值化与局部自适应二值化对比

阈值二值化：

alt

局部自适应二值化：

alt

可以发现，局部自适应的二值化结果内部噪点更少，方便之后的处理；阈值二值化可以手动调整阈值，获得自定义的结果。

两张黑白相反可以调整，对逻辑值取反即可，或者修改阈值二值化的大于小于号

获取图像轮廓

bwboundaries - MathWorks 中国

1
2
contour = bwboundaries(bw_image);% 获取轮廓
boundary = contour{1}; % 取第一个轮廓

[B, L] = bwboundaries(BW) 获取二值化后图像的轮廓，返回由边界像素位置组成的元胞数组 B 和连续区域的标签矩阵 L。

该函数跟踪二值图像 BW 中对象的外边界以及这些对象内部孔洞的边界，具体定义如下：

alt

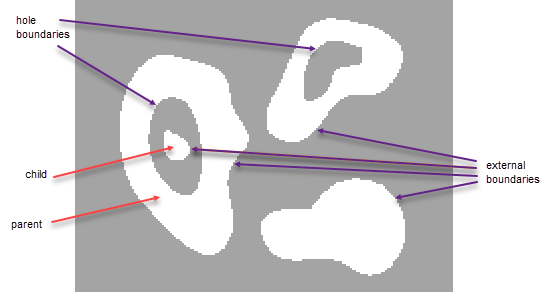
控制连通性

1
B = bwboundaries(BW,conn)

其中 conn 可取4或8，表示使用4联通（上下左右）还是8联通（九宫格）

选择是否寻找内部孔洞

1
2
bwboundaries(BW,'holes');
bwboundaries(BW,'noholes');

官方代码

1
2
3
4
5
6
7
8
9
I = imread('rice.png'); % 读图
BW = imbinarize(I); % 自适应二值化
[B,L] = bwboundaries(BW,'noholes'); % 计算外边界
imshow(label2rgb(L, @jet, [.5 .5 .5])) % 展示图片，使用彩色标记1，中性灰标记0
hold on
for k = 1:length(B)
   boundary = B{k};
   plot(boundary(:,2), boundary(:,1), 'w', 'LineWidth', 2) % 用白线勾勒出边界
end

alt

此外，该函数 [B,L,n,A] = bwboundaries() 还会返回 n（找到的对象数量）和 A（邻接矩阵），可以用于更多用途。

显示图片

1
imshow(bw_image)

表格的读取

读取csv

CSV是一种常见的表格数据格式，其使用逗号分隔数据。

Python读取CSV

1
2
3
import pandas as pd
df = pd.read_csv('file.csv',encoding='gbk')
df = pd.read_excel('file.xlsx', sheet_name='Sheet1')

pd.read_csv() 函数返回一个 DataFrame 对象。其有很多参数：

1
2
3
4
5
6
7
8
9
df = pd.read_csv(
    'data.csv',         # 文件路径
    sep=';',            # 分隔符是分号
    header=0,           # 第一行作为列名
    index_col=0,        # 第一列作为索引
    usecols=['Name', 'Age', 'City'],  # 只读取这三列
    skiprows=[2, 5],    # 跳过第3行和第6行
    na_values=['NA', 'n/a']  # 将'NA'和'n/a'替换为NaN
)
  • sep 用于指定分隔符，默认应该是逗号；
  • header 用于设置表头所在的行，注意Python从0开始计数。如果没有表头，则使用 header=None；
  • index_col 和 header 类似，设置索引所在的行，index_col=0 为设置第一行为索引。如果不设置索引，则 index_col=None；

如果表格不存在列名，可以手动设置列名，索引名也可以设置：

1
2
df.columns = ['Column1', 'Column2', 'Column3']  # 手动设置列名
df.index.name = 'RowIndex'  # 如果想要为索引设置一个名称

Matlab读取表格

不管是txt、csv还是xlsx，都可以通过readtable函数一站式解决，而且其是最灵活的选择，可以处理混合数据类型。

txt+分隔符

1
2
data=readtable('filename.txt','Delimiter','\t');
data=readtable('filename.txt','Delimiter',';');

csv

1
2
3
4
% 读取 CSV 文件到表格变量
data=readtable('filename.csv');
% 访问数据
column1=data.ColumnName1;

xlsx

1
2
3
4
5
6
7
8
9
10
11
data=readtable('filename.xlsx');
% 读取特定工作表
data=readtable('filename.xlsx','Sheet','SheetName');
% 读取特定范围
data=readtable('filename.xlsx','Range','A1:D100');
% 读取所有工作表
[~,sheets]=xlsfinfo('filename.xlsx');
data=cell(1,numel(sheets));
for i=1:numel(sheets)
    data{i}=readtable('filename.xlsx','Sheet',sheets{i});
end

表头与列名

默认情况下，readtable 会将第一行视为表头。 如果表头不在第一行，可以指定表头行

1
data=readtable('filename.csv','HeaderLines',1);  % 表头在第二行

如果文件没有表头，可以设置ReadVariableNames为false

1
data=readtable('filename.csv','ReadVariableNames',false);

自定义列名

1
2
varNames={'Column1','Column2','Column3'};
data=readtable('filename.csv','VariableNames',varNames);

检查和访问表头

1
2
3
4
% 查看变量名
disp(data.Properties.VariableNames);
% 访问特定列
column1=data.Column1;

数据输出

简单的有disp、fprintf，就不展开讲了。

strcat/sprintf组合字符串

设置复杂格式的字符串，用于图片中文字、文件名等地方。

函数

corrcoef皮尔逊相关系数矩阵

基本用法

计算多个列之间的皮尔逊相关系数

1
R=corrcoef(X);

计算两个向量间的相关系数

1
R=corrcoef(x,y);

其还可以返回p值

1
[R,P]=corrcoef(___);

p 值用于判断相关系数是否具有统计显著性。通常，如果 p < 0.05，我们认为相关性是显著的。

找出显著的变量对

1
2
3
[R,P]=corrcoef(X);
% 找出显著相关的变量对
significant_correlations=R.*(P<0.05);

可视化

结合 imagesc 或 heatmap 函数可视化相关矩阵。

1
2
imagesc(R);
heatmap(R);

实例

计算皮尔逊相关系数矩阵，使用imagesc+SIGEWINNE配色可视化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
% 计算皮尔逊相关系数矩阵
R = corrcoef(data);

% 绘制相关系数矩阵的热图
figure;
imagesc(R);
SIGEWINNE=[81 132 178;
    170 212 248;
    242 245 250;
    241 167 181;
    213 82 118]/256;
num_colors = 100; % 插值后的颜色数量
interp_colors = interp1(linspace(0, 1, size(SIGEWINNE, 1)), SIGEWINNE, linspace(0, 1, num_colors));
colormap(interp_colors);
colorbar;
title('皮尔逊相关系数矩阵');
set(gca, 'XTick', 1:7, 'XTickLabel', table_name);
set(gca, 'YTick', 1:7, 'YTickLabel', table_name);
axis square;

% 添加数值标签
textStrings = num2str(R(:), '%0.2f');
textStrings = strtrim(cellstr(textStrings));
[x, y] = meshgrid(1:7);
hStrings = text(x(:), y(:), textStrings(:), 'HorizontalAlignment', 'center');
midValue = mean(get(gca, 'CLim'));
textColors = repmat(R(:) > midValue, 1, 3);
set(hStrings, {'Color'}, num2cell(textColors, 2));

regress多重线性回归

regress 函数用于执行多元线性回归分析，其通过最小二乘法估计回归系数。其基于： \[ \begin{align} y = Xb + \varepsilon \end{align} \]

基本语法

1
[b,bint,r,rint,stats]=regress(y,X);

其中：

  • y 是因变量向量
  • X 是自变量矩阵
  • b 是估计的回归系数
  • bint 是回归系数的置信区间
  • r 是残差
  • rint 是残差的置信区间
  • stats 包含R²、F统计量、p值和误差方差估计

常数项

regress 函数不会自动添加常数项。如果需要常数项，必须手动将其添加到 X 矩阵中，通常作为第一列：

1
X=[ones(size(X,1),1) X];

更复杂的项

需要在调用 regress 之前手动构造 X 矩阵。

1
2
% 假设有两个自变量 x1 和 x2
X=[ones(size(x1)) x1 x2 x1.*x2 x1.^2 x2.^2];

实例

出处：2024江苏省研究生数学建模A题《人造革性能优化设计研究》

3个自变量，创建完全三次项，额外添加常数项，计算R方、MSE，计算t统计量和p值，可视化

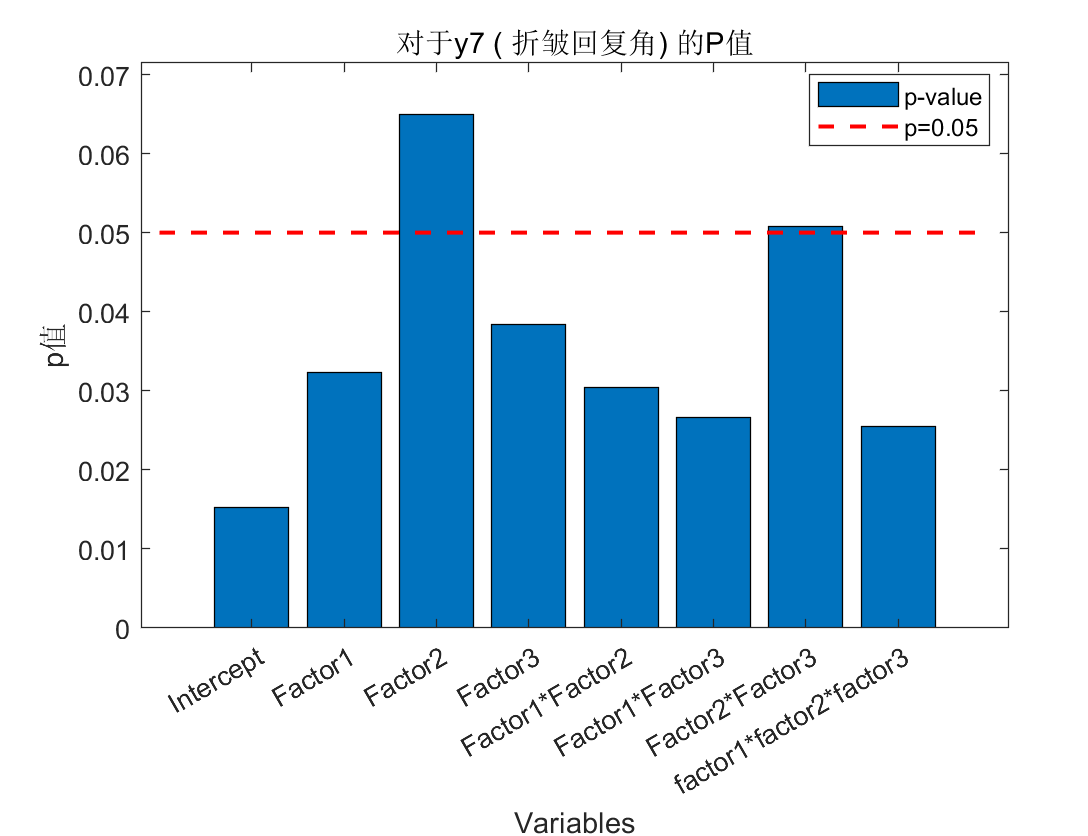
挑选p值最小（最显著的）项绘制散点图并用polyfit作一次趋势线

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
%% 

Y = avg_data;

% 准备因子变量
factors = [factor1' factor2' factor3'];
group = categorical(cellstr(num2str(factors)));

% 创建平方项和交互项
factor1_sq = factor1.^2;
factor2_sq = factor2.^2;
factor3_sq = factor3.^2;
factor1_factor2 = factor1 .* factor2;
factor1_factor3 = factor1 .* factor3;
factor2_factor3 = factor2 .* factor3;

% 创建三次项和高阶交互项
factor1_cub = factor1.^3;
factor2_cub = factor2.^3;
factor3_cub = factor3.^3;
factor1_sq_factor2 = factor1_sq .* factor2;
factor1_factor2_factor3 = factor1 .* factor2 .* factor3;

% 合并所有预测变量（这里按需合并）
% X = [factors, factor1_sq', factor2_sq', factor3_sq', factor1_factor2', factor1_factor3', factor2_factor3',factor1_factor2_factor3'];
X = [factors, factor1_factor2', factor1_factor3', factor2_factor3',factor1_factor2_factor3'];

% var_names = {'Factor1', 'Factor2', 'Factor3', ...
%              'Factor1^2', 'Factor2^2', 'Factor3^2', ...
%              'Factor1*Factor2', 'Factor1*Factor3', 'Factor2*Factor3','factor1*factor2*factor3'};
var_names = {'Factor1', 'Factor2', 'Factor3', ...
             'Factor1*Factor2', 'Factor1*Factor3', 'Factor2*Factor3','factor1*factor2*factor3'};

% 添加常数项
X = [ones(size(X,1),1) X];
var_names = ['Intercept', var_names];

for i = 1:7
    y_i = Y(:, i);
    disp(strcat('Analysis for y', num2str(i), ' (', table_name(i), ')'));
    
    % 多元线性回归
    [b, ~, r, ~, stats] = regress(y_i, X);
    
    % 计算 R^2 和调整后的 R^2
    R2 = stats(1);
    adj_R2 = 1 - (1-R2)*(length(y_i)-1)/(length(y_i)-size(X,2)-1);
    
    % 计算 MSE
    MSE = mean(r.^2);
    
    % 计算每个系数的标准误差
    n = length(y_i);
    p = size(X, 2);
    sigma2 = sum(r.^2) / (n - p);
    C = inv(X' * X);
    se = sqrt(diag(C) * sigma2);
    
    % 计算 t 统计量和 p 值
    t_stat = b ./ se;
    p_values = 2 * (1 - tcdf(abs(t_stat), n - p));
    
    % 显示结果
    disp(['R^2: ', num2str(R2)]);
    disp(['Adjusted R^2: ', num2str(adj_R2)]);
    disp(['MSE: ', num2str(MSE)]);
    disp('Regression coefficients:');
    for j = 1:length(b)
        if b(j) ~= 0
            disp([var_names{j}, ': ', num2str(b(j)), ' (p-value: ', num2str(p_values(j)), ')']);
        end
    end
    
    % 可视化实际值与预测值
    y_pred = X * b;
    figure;
    scatter(y_i, y_pred);
    hold on;
    plot([min(y_i), max(y_i)], [min(y_i), max(y_i)], 'r--');
    xlabel('Actual Values');
    ylabel('Predicted Values');
    title(strcat('Actual vs Predicted for y', num2str(i), ' (', table_name(i), ')'));
    hold off;
    
    % 创建 p 值的柱状图
    figure;
    bar(p_values);
    hold on;
    plot([0, length(p_values)+1], [0.05, 0.05], 'r--', 'LineWidth', 1.5);
    hold off;
    xlabel('Variables');
    ylabel('p值');
    title(strcat('对于y', num2str(i), ' (', table_name(i), ') 的P值'));
    xticks(1:length(var_names));
    xticklabels(var_names);
    xtickangle(30);
    ylim([0, max(max(p_values), 0.05)*1.1]);  % 确保 0.05 线可见
    legend('p-value', 'p=0.05', 'Location', 'best');



    % 找出当前 y_i 中 p 值最小的变量
    [min_p, min_p_index] = min(p_values);

    % 为 p 值最小的变量绘制散点图
    figure;
    scatter(X(:, min_p_index), y_i);
    xlabel(var_names{min_p_index});
    ylabel(['y', num2str(i), ' (', table_name{i}, ')']);
    title(['Relationship between ', var_names{min_p_index}, ...
           ' and y', num2str(i), ' (', table_name{i}, ')']);

    % 添加趋势线
    hold on;
    p = polyfit(X(:, min_p_index), y_i, 1);
    x_trend = linspace(min(X(:, min_p_index)), max(X(:, min_p_index)), 100);
    y_trend = polyval(p, x_trend);
    plot(x_trend, y_trend, 'r--');
    legend('Data points', 'Trend line', 'Location', 'best');
    hold off;

    % 显示最显著变量的信息
    disp(['Most significant variable for y', num2str(i), ': ', var_names{min_p_index}, ...
          ' (p-value: ', num2str(min_p), ')']);
    disp('------------------------');
end

fminunc非线性规划求解器

出处：2023院赛，使用梯度下降求最佳极坐标原点

非线性规划求解器，求无约束多变量函数的最小值。

即求以下问题的最小值： \[ \begin{align} \max_x f(x) \end{align} \] 其中，\(f(x)\) 的返回值为标量，\(x\) 是向量或矩阵

1
2
x = fminunc(fun,x0)
[x,fval] = fminunc(fun,x0,options)

在点 x0 处开始并尝试求 fun 中描述的函数的局部最小值 x，在解 x 处的值为 fval。

options 结构体有许多选项，下面列举几个常用的：

选项 描述
Algorithm 选择 fminunc 算法。选项有“拟牛顿法” quasi-newton（缺省）和“信赖域法” trust-region。如果选 trust-region 的话需要提供梯度，所以一般不变。
Display 显示级别。'off' 或 'none' 不显示输出。'iter' 显示每次迭代的输出，并给出默认退出消息。'iter-detailed' 显示每次迭代的输出，并给出带有技术细节的退出消息。'notify' 仅当函数不收敛时才显示输出，并给出默认退出消息。'final'（默认值）仅显示最终输出，并给出默认退出消息。
PlotFcn 算法执行过程中的各种进度测量值绘图。
MaxIterations 允许的迭代最大次数，为正整数，默认值为 400。

t-SNE

一种降维手段，速度慢，用于聚类后可视化很好

1
2
3
4
5
6
7
load fisheriris
X = meas;
% 运行t-SNE
Y = tsne(X, 'Perplexity', 20, 'NumDimensions', 2);
% 可视化结果
gscatter(Y(:,1), Y(:,2), species)
title('t-SNE Visualization of Iris Dataset')

对于非常大的数据集，MATLAB的t-SNE可能会变慢。在这种情况下，可能需要考虑使用其他优化的实现或降采样数据。

t-SNE与PCA对比

t-SNE的优势

  • 能够捕捉复杂的非线性关系。
  • 擅长保留数据的局部相似性。
  • 适合高维数据的可视化。
  • 能够发现聚类，在低维空间中分离不同的数据簇。

t-SNE的劣势

  • 计算慢，\(O(n^2)\)，而PCA是\(O(\min(n^2d,nd^2))\)的（n个样本与d个特征）。
  • 非确定性：多次运行得到结果不同。
  • 需调参：性能很大程度上依赖于参数设置。
  • 不可逆：无法从降维结果重构原始数据。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
% 加载数据
load fisheriris
X = meas;

% PCA
[coeff,score,latent] = pca(X);
figure;
scatter(score(:,1), score(:,2))
title('PCA of Iris Dataset')

% t-SNE
Y = tsne(X);
figure;
scatter(Y(:,1), Y(:,2))
title('t-SNE of Iris Dataset')

算法

t检验

计算多个x和一个y之间的t统计量和p值

需给出：X, y, var_names, var_names_ch, y_name

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
% 计算每个变量的t统计量和p值
n=length(y);
t_stats=zeros(size(X,2),1);
p_values=zeros(size(X,2),1);

for j=1:size(X,2)
    x_j=X(:,j);
    r=corr(x_j,y);
    t_stats(j)=r*sqrt((n-2)/(1-r^2));
    p_values(j)=2*(1-tcdf(abs(t_stats(j)),n-2));
end

% 显示结果
disp('Variable statistics:');
for j=1:length(var_names)
    disp([var_names{j},': t-stat = ',num2str(t_stats(j)),', p-value = ',num2str(p_values(j))]);
end

% 创建双坐标轴柱状图
figure('Units','centimeters','Position',[0 0 18 14]);
hold on

bar1=[abs(t_stats),zeros(length(var_names),1)];
bar2=[zeros(length(var_names),1),p_values];

yyaxis left;
GO1=bar(bar1);
GO1(1).FaceColor='flat';
GO1(1).CData(t_stats>0,:)=repmat([1,0,0],sum(t_stats>0),1);
GO1(1).CData(t_stats<=0,:)=repmat([0,0,1],sum(t_stats<=0),1);
ylabel('|t值|');
set(gca,'YColor',[.1 .1 .1],'YTick',0:1:10,'Ylim',[0 10]);

yyaxis right;
GO2=bar(bar2);
GO2(2).FaceColor=[0.7 0.7 0.7];
ylabel('p值');
set(gca,'YColor',[.1 .1 .1],'YTick',0:0.05:1,'Ylim',[0 0.5]);

plot([0,length(p_values)+1],[0.05,0.05],'--','LineWidth',1.5,'Color',[0.7 0.7 0.7]);
ylim([0,max(max(p_values),0.05)*1.0]);

set(gca,'Box','off','XGrid','off','YGrid','on','TickDir','out','TickLength',[.01 .01],...
    'XMinorTick','off','YMinorTick','off','XColor',[.1 .1 .1],'Xticklabel',var_names);

title(['各变量关于',y_name,'的t值与p值']);
xticks(1:length(var_names));
xticklabels(var_names_ch);
xtickangle(30);

legend('正t值','负t值','p值','p=0.05','Location','northeast','Orientation','horizontal');
set(gca,'FontName','SimSun','FontSize',12);

% 找出p值最小的变量并绘制散点图
[min_p,min_p_index]=min(p_values);
figure;
scatter(X(:,min_p_index),y);
xlabel(var_names_ch{min_p_index});
ylabel(y_name);
title([var_names_ch{min_p_index},'和',y_name,'之间的关系']);

hold on;
p=polyfit(X(:,min_p_index),y,2);
x_trend=linspace(min(X(:,min_p_index)),max(X(:,min_p_index)),100);
y_trend=polyval(p,x_trend);
plot(x_trend,y_trend,'r--');
legend('实验数据点','趋势线','Location','best');
hold off;

disp(['对于',y_name,'最重要的变量是: ',var_names{min_p_index},...
    ' (p值为: ',num2str(min_p),')']);
end

ANOVA方差分析

Code by AI

以后用到了再修改。

ANOVA 主要用于分析一个或多个离散自变量（通常称为因素）对一个连续因变量的影响。

这些离散自变量通常有几个固定的水平或类别。例如，药物类型（A、B、C）或处理方法（方法1、方法2、方法3）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
% 设置随机种子以确保结果可重复
rng(123);

% 因素水平数量
levels = 3;
repeats = 5;

% 生成因变量 y 的随机数据
% 这里假设因变量 y 受到三个因素及其交互作用的影响
% 我们可以人为地设置一些主效应和交互效应
mu = 10; % 总体均值
effect_size = 2; % 主效应和交互效应大小

% 生成数据
x1 = repmat((1:levels)', [levels*levels*repeats, 1]);
x2 = repmat(repelem((1:levels)', levels), [levels*repeats, 1]);
x3 = repelem((1:levels)', levels*levels*repeats);

% 生成因变量 y
y = mu + ...
    effect_size * (x1 - mean(1:levels)) + ... % 主效应 x1
    effect_size * (x2 - mean(1:levels)) + ... % 主效应 x2
    effect_size * (x3 - mean(1:levels)) + ... % 主效应 x3
    effect_size * (x1 - mean(1:levels)) .* (x2 - mean(1:levels)) + ... % 交互效应 x1:x2
    effect_size * (x1 - mean(1:levels)) .* (x3 - mean(1:levels)) + ... % 交互效应 x1:x3
    effect_size * (x2 - mean(1:levels)) .* (x3 - mean(1:levels)) + ... % 交互效应 x2:x3
    effect_size * (x1 - mean(1:levels)) .* (x2 - mean(1:levels)) .* (x3 - mean(1:levels)) + ... % 三因素交互效应 x1:x2:x3
    randn(size(x1)); % 添加随机噪声

% 进行三因素 ANOVA
[p, tbl, stats] = anovan(y, {x1, x2, x3}, 'model', 'full', 'varnames', {'Factor1', 'Factor2', 'Factor3'});

% 显示 ANOVA 表
disp(tbl);

% 绘制交互效应图
figure;
interactionplot(y, {x1, x2, x3}, 'VarNames', {'Factor1', 'Factor2', 'Factor3'});

k-means聚类

基本用法

1
[cluster_indices,centroids,sumd,distances]=kmeans(normalized_data,K)

实例

出处：2024江苏省研究生数学建模A题《人造革性能优化设计研究》T2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
%% 普通k-means聚类
% 需要提前提供：
% data: 要聚类的数据矩阵
% K: 聚类的数量
% sample_labels: 样本标签（可选，用于显示每个簇中的样本）

% 数据标准化
normalized_data=zscore(data);

% 执行k-means聚类
[cluster_indices,centroids,sumd,distances]=kmeans(normalized_data,K);

% 显示聚类结果
disp('聚类结果（每个样本所属的簇）:');
disp(cluster_indices);

% 计算并显示聚类误差
cluster_errors=sum(sumd);
disp(['K = ',num2str(K),' 时的聚类误差（簇内平方和）为: ',num2str(cluster_errors)]);

% 计算并显示平均轮廓系数
silhouette_values=silhouette(normalized_data,cluster_indices);
mean_silhouette=mean(silhouette_values);
disp(['K = ',num2str(K),' 时的平均轮廓系数为: ',num2str(mean_silhouette)]);

% 计算并显示Calinski-Harabasz指数
ch_index=evalclusters(normalized_data,cluster_indices,'CalinskiHarabasz');
disp(['K = ',num2str(K),' 时的Calinski-Harabasz指数为: ',num2str(ch_index.CriterionValues)]);

% 计算并显示Davies-Bouldin指数
db_index=evalclusters(normalized_data,cluster_indices,'DaviesBouldin');
disp(['K = ',num2str(K),' 时的Davies-Bouldin指数为: ',num2str(db_index.CriterionValues)]);

% 如果提供了样本标签，则显示每个簇中的样本
if exist('sample_labels','var')
    clusters=cell(1,K);
    for i=1:K
        clusters{i}=[];
    end
    
    for i=1:length(cluster_indices)
        clusters{cluster_indices(i)}=[clusters{cluster_indices(i)},sample_labels(i)];
    end
    
    disp('每个簇中的样本:');
    disp(clusters);
end

均衡k-means

出处：2024江苏省研究生数学建模A题《人造革性能优化设计研究》T2

手写的【不完全正确】的均衡k-means函数，调用方法同kmeans()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
function [idx, C,sumd] = capacity_constrained_kmeans(X, K, max_capacity)
    % 初始化
    [n, ~] = size(X);
    idx = zeros(n, 1);
    random_indices = randperm(n, K);
    C = X(random_indices, :);  % 随机选择K个数据点作为初始中心
    
    % 迭代变量
    max_iterations = 100;
    changed = true;
    iteration = 0;
    
    while changed && iteration < max_iterations
        changed = false;
        iteration = iteration + 1;
        
        % 计算所有点到所有簇中心的距离
        distances = pdist2(X, C);
        
        % 创建一个记录每个簇中点的数量的数组
        cluster_sizes = zeros(K, 1);
        
        % 为每个点分配最近的簇，同时考虑簇的容量限制
        for i = 1:n
            % 查找当前点到各个簇中心的距离排序
            [~, sorted_indices] = sort(distances(i, :));
            
            for j = 1:K
                closest_cluster = sorted_indices(j);
                if cluster_sizes(closest_cluster) < max_capacity
                    if idx(i) ~= closest_cluster
                        changed = true;
                    end
                    idx(i) = closest_cluster;
                    cluster_sizes(closest_cluster) = cluster_sizes(closest_cluster) + 1;  % 新簇数量增加
                    break;
                end
            end
        end
        
        % 更新簇中心
        for j = 1:K
            if any(idx == j)
                C(j, :) = mean(X(idx == j, :), 1);
            end
        end
    end


    % 计算簇内平方和 (sumd)
    sumd = zeros(K, 1);
    for j = 1:K
        cluster_points = X(idx == j, :);
        sumd(j) = sum(sum((cluster_points - C(j, :)).^2, 2));
    end
    
    % 确保所有数据点都被分配
    if any(idx == 0)
        warning('Some points were not assigned to any cluster due to capacity constraints.');
    end
end

随机森林+变量重要性排序+OOB+网格搜索

绘图

为了区别“图片”的“图”和“图论”的“图”，故用Graph代指“由若干给定的顶点及连接两顶点的边所构成的图形”。

networkx绘制Graph

出处：2024MathorCup，快递节点之间物流量可视化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import networkx as nx
import matplotlib.pyplot as plt

# 创建一个空的有向图
G = nx.DiGraph()

# 从 DataFrame 添加边到图中
for idx, row in edges_df.iterrows():
    G.add_edge(row['始发分拣中心'], row['到达分拣中心'], weight=edge_weight)
# weight=row['货量']
# 如果没有权重，可以省略 weight 属性

# 使用多种算法计算节点位置
pos = nx.spring_layout(G) # k 值较大可以增加节点之间的距离
pos = nx.spring_layout(G, k=0.01, iterations=20)  
pos = nx.spectral_layout(G)
pos = nx.shell_layout(G)

# 绘制图，包括节点标签和透明度设置
nx.draw(G, pos, with_labels=True, node_size=100, font_size=10,alpha=0.4,edge_color='gray')

# 获取并绘制所有边的权重标签
#edge_weights = nx.get_edge_attributes(G, 'weight')
#nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_weights)
#nx.draw_networkx_edge_labels(G, pos, edge_labels="")

# 显示图形
plt.show()

Matlab设置画图背景为白色

1
set(gcf, 'Color', 'w');

一般情况，复制到word的话，并不需要这个，直接点击“复制图窗”就好。这个可以用于截图。

数据散点图

出处：2024江苏省研究生数学建模A题《人造革性能优化设计研究》T2

16个实验，每次实验重复3次，得到了48个数据点。同一组实验的三个数据点赋予相同的颜色。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
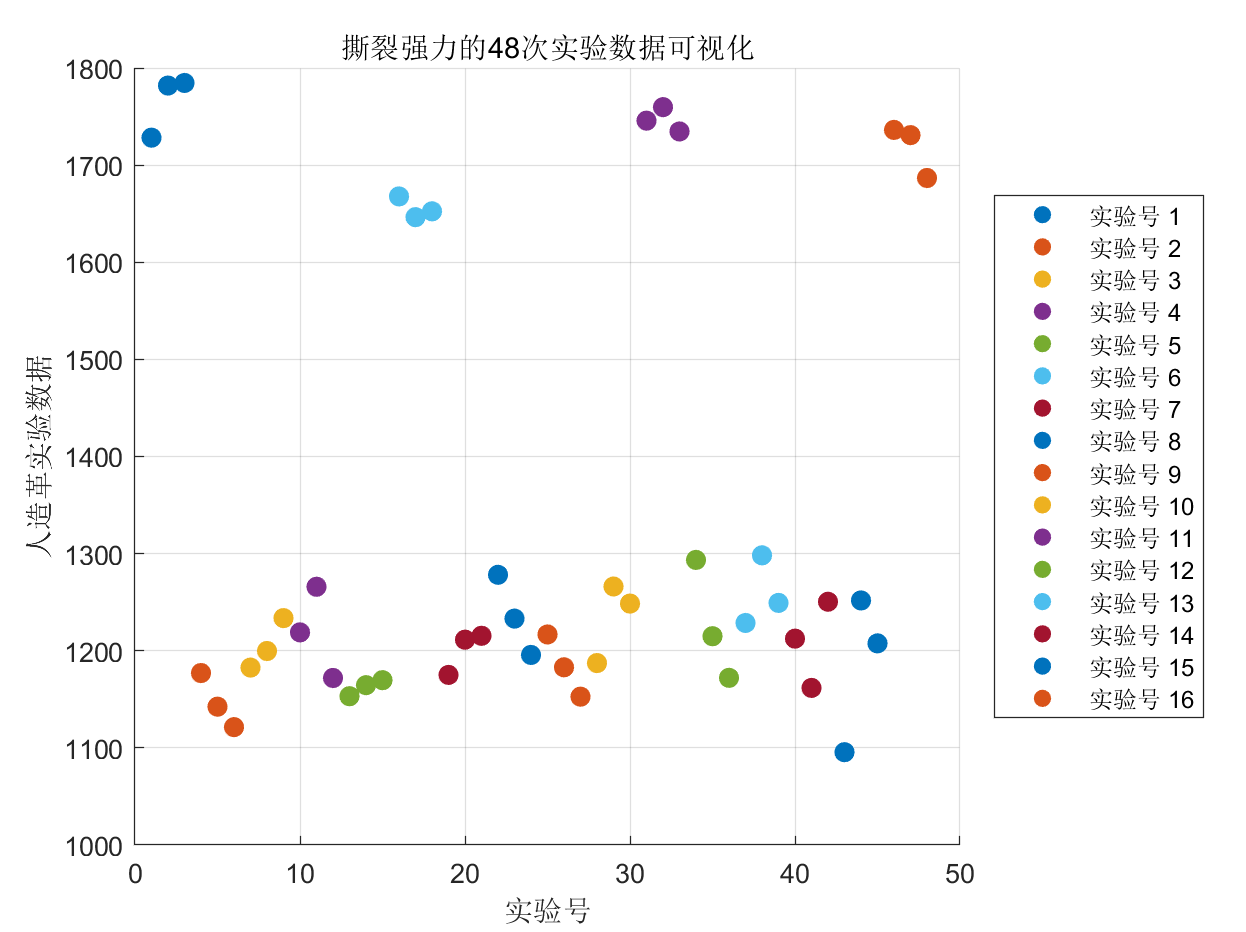
16
colors = lines(16);
figure;
hold on;
for i = 1:3:length(data)
    color_idx = ceil(i/3);
    scatter(i:i+2, data(i:i+2), 50, 'MarkerEdgeColor', colors(color_idx, :), 'MarkerFaceColor', colors(color_idx, :), 'DisplayName', sprintf('实验号 %d', color_idx));
end

legend show;
legend('Location', 'eastoutside');
title(strcat(table_name(table_num),"的48次实验数据可视化"));
xlabel('实验号');
ylabel('人造革实验数据');
grid on;
set(gcf, 'Color', 'w');
hold off;

双柱状图

学习自：阿昆的科研日常

出处：2024江苏省研究生数学建模A题《人造革性能优化设计研究》T2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
% 创建双坐标轴柱状图
figure('Units','centimeters','Position',[0 0 18 14]);
hold on

bar1=[abs(t_stats),zeros(length(var_names),1)];
bar2=[zeros(length(var_names),1),p_values];

yyaxis left;
GO1=bar(bar1);
GO1(1).FaceColor='flat';
GO1(1).CData(t_stats>0,:)=repmat([1,0,0],sum(t_stats>0),1);
GO1(1).CData(t_stats<=0,:)=repmat([0,0,1],sum(t_stats<=0),1);
ylabel('|t值|');
set(gca,'YColor',[.1 .1 .1],'YTick',0:1:10,'Ylim',[0 10]);

yyaxis right;
GO2=bar(bar2);
GO2(2).FaceColor=[0.7 0.7 0.7];
ylabel('p值');
set(gca,'YColor',[.1 .1 .1],'YTick',0:0.05:1,'Ylim',[0 0.5]);

plot([0,length(p_values)+1],[0.05,0.05],'--','LineWidth',1.5,'Color',[0.7 0.7 0.7]);
ylim([0,max(max(p_values),0.05)*1.0]);

set(gca,'Box','off','XGrid','off','YGrid','on','TickDir','out','TickLength',[.01 .01],...
    'XMinorTick','off','YMinorTick','off','XColor',[.1 .1 .1],'Xticklabel',var_names);

title(['各变量关于',y_name,'的t值与p值']);
xticks(1:length(var_names));
xticklabels(var_names_ch);
xtickangle(30);

legend('正t值','负t值','p值','p=0.05','Location','northeast','Orientation','horizontal');
set(gca,'FontName','SimSun','FontSize',12);

三维柱状图

学习自：阿昆的科研日常

出处：2024江苏省研究生数学建模A题《人造革性能优化设计研究》T3T4

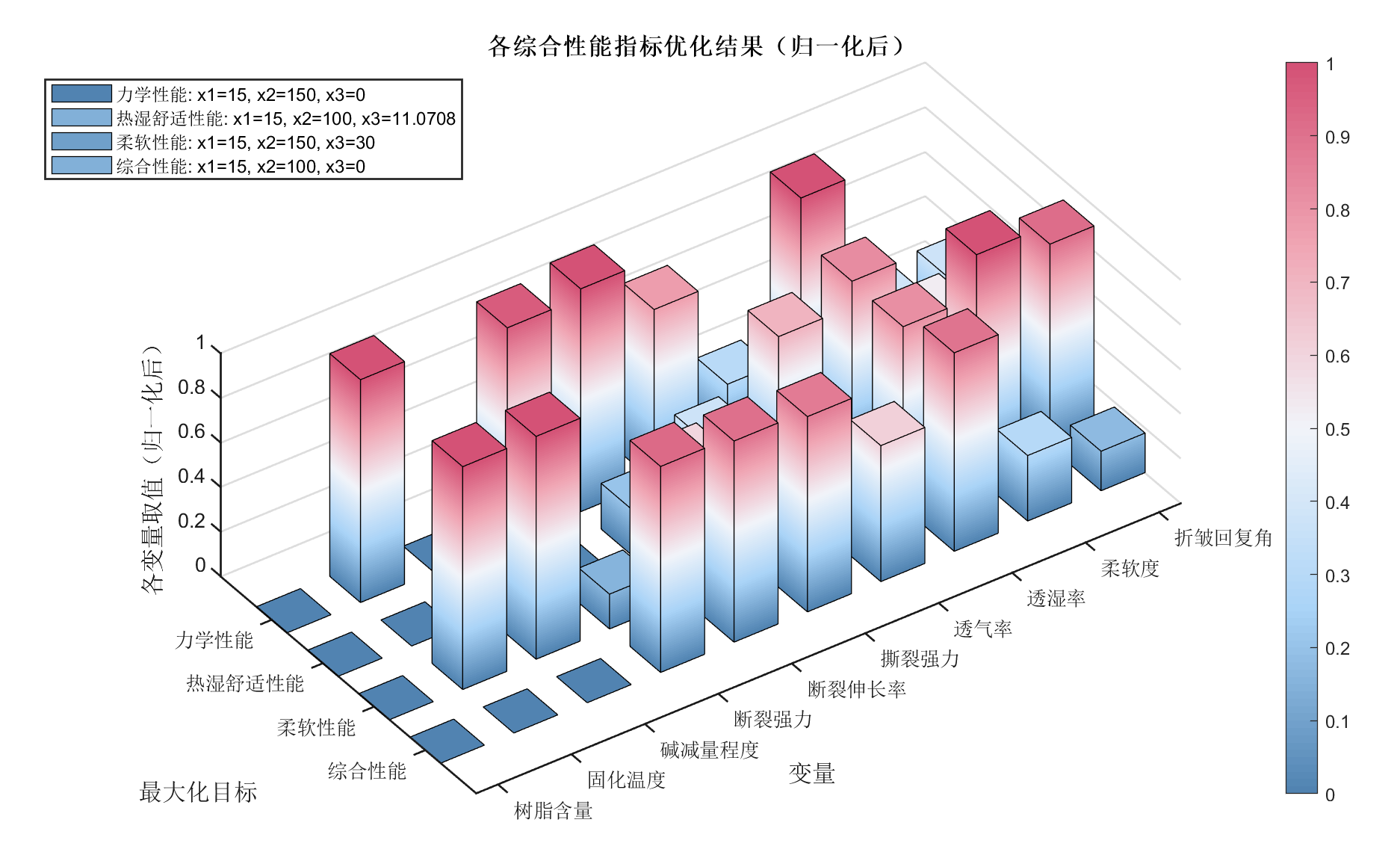
输入变量：X行Y列矩阵optimized_results

下述代码有四个部分：

  1. 渲染SIGEWINNE
  2. 正常的绘图
  3. 值域归一化后绘图（效果见上图）
  4. 对数化后绘图（效果见上图）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
%% SIGEWINNE

SIGEWINNE=[81 132 178;
    170 212 248;
    242 245 250;
    241 167 181;
    213 82 118]/256;
num_colors = 100; % 插值后的颜色数量
interp_colors = interp1(linspace(0, 1, size(SIGEWINNE, 1)), SIGEWINNE, linspace(0, 1, num_colors));

%% 画图-普通


% colormap(jet(64));  % 或者使用其他内置颜色图，如 parula, hsv 等
colormap(interp_colors);
% 绘制三维柱状图
figureHandle = figure;
GO = bar3(optimized_results(:,4:end), 0.6);  % 只使用 y1-y7 的数据
hTitle = title('Optimization Results for z1, z2, z3, z4');
hXLabel = xlabel('Variables');
hYLabel = ylabel('Optimization Case');
hZLabel = zlabel('Value');

% 细节优化
% 坐标区调整
set(gca, 'Box', 'off', ...
         'LineWidth', 1, 'GridLineStyle', '-',...
         'XGrid', 'off', 'YGrid', 'off', 'ZGrid', 'on', ...
         'TickDir', 'out', 'TickLength', [.015 .015], ...
         'XMinorTick', 'off', 'YMinorTick', 'off',  'ZMinorTick', 'off',...
         'XColor', [.1 .1 .1],  'YColor', [.1 .1 .1], 'ZColor', [.1 .1 .1],...
         'Xticklabel', {'y1', 'y2', 'y3', 'y4', 'y5', 'y6', 'y7'}, ...
         'Yticklabel', {'z1', 'z2', 'z3', 'z4'})

% 字体和字号
set(gca, 'FontName', 'Helvetica')
set([hXLabel, hYLabel, hZLabel], 'FontName', 'AvantGarde')
set(gca, 'FontSize', 10)
set([hXLabel, hYLabel, hZLabel], 'FontSize', 12)
set(hTitle, 'FontSize', 12, 'FontWeight' , 'bold')

% 背景颜色
set(gcf, 'Color', [1 1 1])

% 添加 x1, x2, x3 的信息到图例
legendStr = cell(4,1);
for i = 1:4
    legendStr{i} = sprintf('z%d: x1=%.2f, x2=%.2f, x3=%.2f', ...
                           i, optimized_results(i,1), optimized_results(i,2), optimized_results(i,3));
end
legend(legendStr, 'Location', 'eastoutside')

% 调整图形大小以适应所有元素
set(gcf, 'Position', [100, 100, 1000, 600])

%% 画图-归一化

y=calc_y(lb);
z=calc_z(lb);
y_min=y;
y_max=y;
z_min=z;
z_max=z;
for fac1=linspace(lb(1),ub(1),10)
    for fac2=linspace(lb(2),ub(2),10)
        for fac3=linspace(lb(3),ub(3),10)
            % [y,z]=objective_ord([fac1,fac2,fac3]);
            y=calc_y([fac1,fac2,fac3]);
            z=calc_z([fac1,fac2,fac3]);
            y_min=min([y_min;y]);
            y_max=max([y_max;y]);
            z_min=min([z_min;z]);
            z_max=max([z_max;z]);
        end
    end
end



% 假设 optimized_results 已经包含了归一化后的数据
% x1, x2, x3 的归一化
x_normalized = (optimized_results(:,1:3) - lb) ./ (ub - lb);

% y1-y7 的归一化 (假设已经在 optimized_results 中)
y_normalized = (optimized_results(:,4:end) - y_min) ./ (y_max - y_min);

% 合并归一化数据
normalized_data = [x_normalized, y_normalized];


figureHandle = figure;
% colormap(jet(64));
colormap(interp_colors);

% 绘制三维柱状图
GO = bar3(normalized_data, 0.6);

% 为每个柱子设置颜色
for i = 1:length(GO)
    zdata = GO(i).ZData;
    GO(i).CData = zdata;
    GO(i).FaceColor = 'interp';
end

% 创建标题和标签
hTitle = title('各综合性能指标优化结果（归一化后）');
hXLabel = xlabel('变量');
hYLabel = ylabel('最大化目标');
hZLabel = zlabel('各变量取值（归一化后）');

% 坐标区调整
set(gca, 'Box', 'off', ...
         'LineWidth', 1, 'GridLineStyle', '-',...
         'XGrid', 'off', 'YGrid', 'off', 'ZGrid', 'on', ...
         'TickDir', 'out', 'TickLength', [.015 .015], ...
         'XMinorTick', 'off', 'YMinorTick', 'off',  'ZMinorTick', 'off',...
         'XColor', [.1 .1 .1],  'YColor', [.1 .1 .1], 'ZColor', [.1 .1 .1],...
         'Xticklabel', {'树脂含量','固化温度','碱减量程度','断裂强力', '断裂伸长率', '撕裂强力', '透气率', '透湿率', '柔软度', '折皱回复角'}, ...
         'Yticklabel', {'力学性能', '热湿舒适性能', '柔软性能', '综合性能'})

% 字体和字号
set(gca, 'FontName', 'Helvetica')
set([hXLabel, hYLabel, hZLabel], 'FontName', 'AvantGarde')
set(gca, 'FontSize', 10)
set([hXLabel, hYLabel, hZLabel], 'FontSize', 12)
set(hTitle, 'FontSize', 12, 'FontWeight' , 'bold')

% 背景颜色
set(gcf, 'Color', [1 1 1])

% 添加颜色条
colorbar

% 添加 x1, x2, x3 的信息到图例
legendStr = cell(4,1);
for i = 1:4
    legendStr{i} = sprintf('%s: x1=%g, x2=%g, x3=%g', ...
                           z_name{i}, optimized_results(i,1), optimized_results(i,2), optimized_results(i,3));
end
legend(legendStr, 'Location', 'eastoutside')

% 调整图形大小以适应所有元素
set(gcf, 'Position', [100, 100, 1000, 600])



%% 画图-LOG

% 使用对数刻度处理数据
log_data = log10(abs(optimized_results) + 1);  % 加1避免log(0)
log_data = log_data .* sign(optimized_results);  % 恢复正负号



% 绘制三维柱状图
figureHandle = figure;
GO = bar3(log_data, 0.6);

% 创建颜色映射
colormap(jet(64));

% 为每个柱子设置颜色
for i = 1:length(GO)
    zdata = GO(i).ZData;
    GO(i).CData = zdata;
    GO(i).FaceColor = 'interp';
end

% 创建标题和标签，并保存句柄
hTitle = title('Optimization Results for z1, z2, z3, z4 (Log Scale)');
hXLabel = xlabel('Variables');
hYLabel = ylabel('Optimization Case');
hZLabel = zlabel('Log10(|Value| + 1)');

% 细节优化
% 坐标区调整
set(gca, 'Box', 'off', ...
         'LineWidth', 1, 'GridLineStyle', '-',...
         'XGrid', 'off', 'YGrid', 'off', 'ZGrid', 'on', ...
         'TickDir', 'out', 'TickLength', [.015 .015], ...
         'XMinorTick', 'off', 'YMinorTick', 'off',  'ZMinorTick', 'off',...
         'XColor', [.1 .1 .1],  'YColor', [.1 .1 .1], 'ZColor', [.1 .1 .1],...
         'Xticklabel', {'factor1','factor2','factor3','y1', 'y2', 'y3', 'y4', 'y5', 'y6', 'y7'}, ...
         'Yticklabel', {'z1', 'z2', 'z3', 'z4'})

% 字体和字号
set(gca, 'FontName', 'Helvetica')
set([hXLabel, hYLabel, hZLabel], 'FontName', 'AvantGarde')
set(gca, 'FontSize', 10)
set([hXLabel, hYLabel, hZLabel], 'FontSize', 12)
set(hTitle, 'FontSize', 12, 'FontWeight' , 'bold')

% 背景颜色
set(gcf, 'Color', [1 1 1])

% 添加颜色条
colorbar

% 添加 x1, x2, x3 的信息到图例
legendStr = cell(4,1);
for i = 1:4
    legendStr{i} = sprintf('z%d: x1=%.2f, x2=%.2f, x3=%.2f', ...
                           i, optimized_results(i,1), optimized_results(i,2), optimized_results(i,3));
end
legend(legendStr, 'Location', 'eastoutside')

% 调整图形大小以适应所有元素
set(gcf, 'Position', [100, 100, 1000, 600])

完整实例

pytorch实现BP神经网络

出处：2024MathorCup-C《物流网络分拣中心货量预测及人员排班》T1使用神经网络对每个快递节点预测每时段的处理量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
import torch
import torch.nn as nn
import torch.optim as optim

# 定义一个简单的神经网络类
class SimpleNN(nn.Module):
    def __init__(self):
        super(SimpleNN, self).__init__()
        self.fc1 = nn.Linear(2, 5)  # 输入层到隐藏层
        self.fc2 = nn.Linear(5, 1)  # 隐藏层到输出层
        self.relu = nn.ReLU()  # 激活函数

    def forward(self, x):
        x = self.relu(self.fc1(x))  # 第一个全连接层和激活函数
        x = self.fc2(x)  # 输出层
        return x


# 创建神经网络实例
model = SimpleNN()

# 定义损失函数和优化器
criterion = nn.MSELoss()  # MSE损失函数
optimizer = optim.SGD(model.parameters(), lr=0.01)  # 选择优化器，设置lr

# 从其他地方得到的数据
dates = list(sc_data[sc].keys())
inputs_raw = torch.tensor([sc_data[sc][date]['总货量'] for date in dates]).float().view(-1, 1)
targets = torch.tensor([sc_data[sc][date]['小时数据'] for date in dates]).float()

# 二值化
min_val = inputs_raw.min()
max_val = inputs_raw.max()
inputs = (inputs_raw - min_val) / (max_val - min_val)


# 构造一个简单的数据集（输入-输出）
inputs = torch.tensor([[0, 0], [0, 1], [1, 0], [1, 1]], dtype=torch.float32)
labels = torch.tensor([[0], [1], [1], [0]], dtype=torch.float32)

# 训练模型
epochs = 10000
for epoch in range(epochs):
    # 前向传播
    outputs = model(inputs)
    loss = criterion(outputs, labels)

    # 反向传播和优化
    optimizer.zero_grad()  # 梯度清零
    loss.backward()  # 反向传播
    optimizer.step()  # 更新参数

    if (epoch + 1) % 100 == 0:
        print(f'Epoch [{epoch + 1}/{epochs}], Loss: {loss.item():.4f}')

# 测试模型
with torch.no_grad():
    test_input = torch.tensor([[0, 0], [0, 1], [1, 0], [1, 1]], dtype=torch.float32)
    predicted = model(test_input)
    print("Test Predictions:")
    print(predicted)

stepwisefit.Keep+可视化+PSO可视化

出处：2024江苏省研究生数学建模A题《人造革性能优化设计研究》T2

7个y和3个x，使用stepwisefit函数进行强制包含一次项的逐步回归，计算R²、MSE等统计量，生成回归表达式；

绘制预测值vs实际值散点图和残差图

image-20240904103048632

使用particleswarm函数寻找最优解

自定义绘图函数myPlotFcn展示优化过程

粒子群可视化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
close all;
clc;
clear;
global b_global;
global intercept_global;
global inmodel_global;
global cnt;
global factor123_global;
global table_num_global;
table_name=["断裂强力","断裂伸长率","撕裂强力","透气率","透湿率","柔软度","折皱回复角"];
data=zeros(48,7);
avg_data=zeros(16,7);
for i=1:7
    table1=readtable(strcat("data_process\data_process_",num2str(i),".xlsx"));
    data(:,i)=table2array(table1);
    for j=1:3:48
        avg_data(ceil(j/3),i)=mean(data(j:j+2,i));
    end
end

% 生成每个样本的参数
factor1=[ones(1,4)*15,ones(1,4)*20,ones(1,4)*25,ones(1,4)*30];
factor2=[100,110,120,130];
factor2=[factor2,factor2,factor2,factor2];
factor3=[0,1,2,3,1,0,3,2,2,3,0,1,3,2,1,0].*10;
factor1_ord=[15,20,25,30];
factor2_ord=factor2(1:4);
factor3_ord=factor3(1:4);

lb = [15,100,0];
% ub = [30,130,30];
ub = [35,150,30];
factor123_global=[lb;ub];

%% factor
X=calc([factor1',factor2',factor3']);

var_names = {'Factor1', 'Factor2', 'Factor3', ...
             'Factor1^2', 'Factor2^2', 'Factor3^2', ...
             'Factor1*Factor2', 'Factor1*Factor3', 'Factor2*Factor3', ...
              'Factor1^3', 'Factor2^3', 'Factor3^3', ...
             'Factor1^2*Factor2', 'Factor1^2*Factor3', ...
             'Factor2^2*Factor1', 'Factor2^2*Factor3', ...
             'Factor3^2*Factor1', 'Factor3^2*Factor2', ...
             'Factor1*Factor2*Factor3'};
var_names_ch = {'因素1', '因素2', '因素3', ...
             '因素1^2', '因素2^2', '因素3^2', ...
             '因素1*因素2', '因素1*因素3', '因素2*因素3', ...
             '因素1^3', '因素2^3', '因素3^3', ...
             '因素1^2*因素2', '因素1^2*因素3', ...
             '因素2^2*因素1', '因素2^2*因素3', ...
             '因素3^2*因素1', '因素3^2*因素2', ...
             '因素1*因素2*因素3'};

%% stepwisefit

table_ans=table();

for table_num=1:7
    fprintf("回归y_%d（%s）\n",table_num,table_name(table_num));
    y=avg_data(:,table_num);

    % start_inmodel_all=[true(1,width(var_names))];
    start_inmodel123=[true(1,3),false(1,width(var_names)-3)];
    [b, se, pval, inmodel, stats, nextstep, history] = stepwisefit(X, y,'InModel',start_inmodel123,'Keep',start_inmodel123, 'penter', 0.05, 'premove', 0.1, 'display', 'on');
    
    % 强制一次项

    % inmodel(1:3)=ones(1,3);
    % XX=[X(:,inmodel),ones(height(X),1)];
    % [bb, ~, ~, ~, stats] = regress(y, XX);
    % 
    % b = zeros(size(X, 2), 1);
    % b(inmodel)=bb(1:end-1);
    


    % 获取截距
    intercept = stats.intercept;
    % intercept=bb(end);

    % 选择的模型
    selected_model = X(:, inmodel);
    
    % 预测
    y_pred = selected_model * b(inmodel) + intercept;
    
    % 计算 R^2
    SST = sum((y - mean(y)).^2);
    SSE = sum((y - y_pred).^2);
    R2 = 1 - SSE/SST;
    
    % 计算 MSE
    MSE = mean((y - y_pred).^2);
    
    % 显示结果
    fprintf('R^2: %.4f\n', R2);
    fprintf('MSE: %.4f\n', MSE);
    
    % 构建回归表达式
    selected_var = find(inmodel);
    expression = 'Y = ';
    for i = 1:sum(inmodel)
        if i == 1
            expression = strcat(expression, sprintf('%.4f*%s', b(selected_var(i))), var_names_ch(selected_var(i)));
        else
            expression = strcat(expression, sprintf(' + %.4f*%s', b(selected_var(i))), var_names_ch(selected_var(i)));
        end
    end
    expression = strcat(expression, sprintf(' + %.4f', intercept));
    
    % 显示表达式
    disp('回归表达式:');
    disp(expression);
    
    
    %% table
    if iscell(var_names)
        var_names = string(var_names);
    end

    
    % 创建一个逻辑向量,表示每个变量是否被选中
    selected = zeros(length(var_names), 1);
    selected(inmodel) = 1;
    
    % 创建一个向量,存储每个变量的系数
    coefficients = zeros(length(var_names), 1);
    coefficients(inmodel) = b(inmodel);
    
    % 创建表格
    table_data = table(var_names', selected, coefficients, 'VariableNames', {'Variable', 'Selected', 'Coefficient'});

    % 添加常数项
    table_data = [table_data; {'Intercept', 1, intercept}];
    
    % 显示表格
    disp(table_data);

    writetable(table_data, sprintf('problem2/y%d.xlsx', table_num));



    %% 可视化
    
    % 创建一个新的图形窗口
    figure('Position', [100, 100, 500, 800]);
    
    % 1. 预测值vs实际值散点图
    subplot(4, 1, [1,2,3]);
    scatter(y, y_pred, 50, 'filled', 'MarkerFaceColor', [0.3 0.6 0.9], 'MarkerEdgeColor', 'none');
    hold on;
    
    % 计算坐标轴范围
    min_val = min(min(y), min(y_pred));
    max_val = max(max(y), max(y_pred));
    range = max_val - min_val;
    axis_min = min_val - range * 0.05;
    axis_max = max_val + range * 0.05;
    
    % 添加y=x的对角线
    plot([axis_min, axis_max], [axis_min, axis_max], 'r--', 'LineWidth', 2);
    
    xlabel('实际值', 'FontSize', 12);
    ylabel('预测值', 'FontSize', 12);
    title('预测值 -- 实际值 拟合散点图', 'FontSize', 14);
    grid on;
    axis square;
    axis([axis_min, axis_max, axis_min, axis_max]);
    
    % 添加R^2值到图中
    text(axis_min, axis_max, sprintf('R^2 = %.4f', R2), 'FontSize', 12, 'VerticalAlignment', 'top');
    
    % 2. 残差图
    subplot(4, 1, 4);
    residuals = y - y_pred;
    scatter(y_pred, residuals, 50, 'filled', 'MarkerFaceColor', [0.3 0.6 0.9], 'MarkerEdgeColor', 'none');
    hold on;
    
    % 计算残差图的坐标轴范围
    res_min = min(residuals);
    res_max = max(residuals);
    res_range = res_max - res_min;
    res_axis_min = res_min - res_range * 0.05;
    res_axis_max = res_max + res_range * 0.05;
    
    % 添加y=0的水平线
    plot([axis_min, axis_max], [0, 0], 'r--', 'LineWidth', 2);
    
    xlabel('预测值', 'FontSize', 12);
    ylabel('残差', 'FontSize', 12);
    title('残差图', 'FontSize', 14);
    grid on;
    axis([axis_min, axis_max, res_axis_min, res_axis_max]);
    
    % 调整图形外观
    set(gcf, 'Color', 'w');
    set(findall(gcf,'-property','FontName'),'FontName', 'SimSun');
    
    % 添加整体标题
    sgtitle(sprintf('回归模型效果评估 - %s', table_name(table_num)), 'FontSize', 16);
    
    % 保存图形
    % saveas(gcf, sprintf('problem2/regression_evaluation_y%d.png', table_num));



    %% PSO求极值

    b_global = b;
    intercept_global = intercept;
    inmodel_global = inmodel;
    cnt=0;
    table_num_global=table_num;

    nvars = 3;
    options = optimoptions('particleswarm','MinNeighborsFraction',0.8,'SwarmSize',100);
    
    options = optimoptions(options,'PlotFcn',@myPlotFcn); % 自定义绘图函数
    % options = optimoptions(options,'PlotFcn',@pswplotbestf); % 默认绘图函数
    [x_best,fval] = particleswarm(@fun,nvars,lb,ub,options)



    %% 添加新列

    newRow = {table_name(table_num),R2, MSE, expression{1},-fval, x_best(1),x_best(2),x_best(3)};
    table_ans = [table_ans; newRow];

    
end



% 为表格设置列名
table_ans.Properties.VariableNames = {'性能指标','R2', 'MSE', '表达式', '最优值', 'x1', 'x2', 'x3'};

% 显示最终表格
disp(table_ans);

writetable(table_ans,"problem2/all.xlsx");

function yidatuo=calc(factors)
    % 构造一大堆
    factor1=factors(:,1);
    factor2=factors(:,2);
    factor3=factors(:,3);
    factor1_sq = factor1.^2;
    factor2_sq = factor2.^2;
    factor3_sq = factor3.^2;
    factor1_factor2 = factor1 .* factor2;
    factor1_factor3 = factor1 .* factor3;
    factor2_factor3 = factor2 .* factor3;
    factor1_cub = factor1.^3;
    factor2_cub = factor2.^3;
    factor3_cub = factor3.^3;
    factor1_sq_factor2 = factor1_sq .* factor2;
    factor1_sq_factor3 = factor1_sq .* factor3;
    factor2_sq_factor1 = factor2_sq .* factor1;
    factor2_sq_factor3 = factor2_sq .* factor3;
    factor3_sq_factor1 = factor3_sq .* factor1;
    factor3_sq_factor2 = factor3_sq .* factor2;
    factor1_factor2_factor3 = factor1 .* factor2 .* factor3;
    X = factors;
    X=[X,factor1_sq, factor2_sq, factor3_sq];
    X=[X, factor1_factor2, factor1_factor3, factor2_factor3];
    X=[X,factor1_cub, factor2_cub, factor3_cub];
    X=[X,factor1_sq_factor2,factor1_sq_factor3,factor2_sq_factor1,factor2_sq_factor3,factor3_sq_factor1,factor3_sq_factor2, factor1_factor2_factor3];
    
    yidatuo=X;
end

function res=fun(factors) % x应该是三变量的
    global b_global;
    global intercept_global;
    global inmodel_global;

    X=calc(factors);
    selected_model = X(:, inmodel_global);
    y_pred = selected_model * b_global(inmodel_global) + intercept_global;
    res=-y_pred;
end







function stop = myPlotFcn(optimValues, state)
    global cnt;
    global factor123_global;
    global table_num_global;
    % pause(0.05); % 停2s,方便截图
    % disp(state);
    stop = false;
    switch state
        case 'init'
            hold on;
            xlabel('因素1');
            ylabel('因素2');
            zlabel('因素3');
            title(['性能指标',num2str(table_num_global),'第',num2str(cnt),'次迭代过程中的粒子位置']);
            
            xlim(factor123_global(:,1));
            ylim(factor123_global(:,2));
            zlim(factor123_global(:,3));
            view(3); % Set 3D view
            grid on;
        case 'iter'
            
            cla;
            title(['性能指标',num2str(table_num_global),'第',num2str(cnt),'次迭代过程中的粒子位置']);
            
            % Plot all particle positions
            scatter3(optimValues.swarm(:,1), optimValues.swarm(:,2), optimValues.swarm(:,3),10,'b', 'filled');
            % disp(size(optimValues.swarm))
            % Highlight the best particle position
            scatter3(optimValues.bestx(1), optimValues.bestx(2), optimValues.bestx(3), 20, 'r', 'filled');
            
            xlim(factor123_global(:,1));
            ylim(factor123_global(:,2));
            zlim(factor123_global(:,3));
            view(3);
            grid on;
            drawnow;

            % 在第4次迭代时保留图形
            if cnt == 4
                saveas(gcf, sprintf('problem2/性能指标%dPSO迭代4次.png', table_num_global)); % 保存图形
            end
            cnt = cnt + 1;
        case 'done'
            hold off;
    end
end

pytorch+RNN手写数字集分类

Code by wyy

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
import torch
import torch.nn as nn
import torchvision.transforms as transforms
import torchvision.datasets as datasets
import torchvision
import numpy as np
import matplotlib.pyplot as plt
from torch import device

trainsets = datasets.MNIST(root="./data", train=True, download=True, transform=transforms.ToTensor())
testsets = datasets.MNIST(root="./data", train=False, transform=transforms.ToTensor())
class_names = trainsets.classes

BATCH_SIZE = 32  # 每批读取的数据大小
EPOCHS = 10  # 训练10轮
train_loader = torch.utils.data.DataLoader(dataset=trainsets, batch_size=BATCH_SIZE, shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=testsets, batch_size=BATCH_SIZE, shuffle=True)
#查看一批batch数据
images, labels = next(iter(test_loader))
print(images.shape)
print(labels.shape)

def imshow(inp,title=None):
    inp = inp.numpy().transpose((1, 2, 0))
    mean = np.array([0.485, 0.456, 0.406])
    std = np.array([0.229, 0.224, 0.225])
    inp = std * inp + mean
    inp = np.clip(inp, 0, 1)
    plt.imshow(inp)
    if title is not None:
        plt.title(title)
    plt.pause(0.001)
    plt.show()
    #网格显示
    out=torchvision.utils.make_grid(images)
    imshow(out)

class RNN_Model(nn.Module):
    def __init__(self, input_dim, hidden_dim, layer_dim, output_dim, h0=None):
        super(RNN_Model,self).__init__()
        self.hidden_dim = hidden_dim
        self.layer_dim = layer_dim
        self.rnn=nn.RNN(input_dim,hidden_dim,layer_dim,batch_first=True,nonlinearity='relu')
        #全连接层
        self.fc = nn.Linear(hidden_dim,output_dim)

    def forward(self,x):
        #layer_dim,batch_size,hidden_dim
        h0=torch.zeros(self.layer_dim,x.size(0),self.hidden_dim).requires_grad_().to(device)
        #分离隐藏状态，避免梯度爆炸
        out,hn=self.rnn(x,h0.detach())
        out = self.fc(out[:,-1,])
        return out
input_dim = 28
hidden_dim = 100
layer_dim = 2
output_dim = 10
model = RNN_Model(input_dim, hidden_dim, layer_dim, output_dim)
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
#损失函数
criterion = nn.CrossEntropyLoss()
#优化器
learning_rate = 0.01
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
#模型参数
I=len(list(model.parameters()))
for i in range(I):
    print("参数：%d"%(i+1))
    print(list((model.parameters()))[i].size())
#模型训练
sequence_dim=28
loss_list=[]
accuracy_list=[]
iteration_list=[]
iter=0
for epoch in range(EPOCHS):
    for i, (images, labels) in enumerate(train_loader):
        model.train()
        images, labels = images.view(-1,sequence_dim,input_dim).requires_grad_().to(device), labels.to(device)
        optimizer.zero_grad()
        outputs = model(images)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()
        iter+=1
#模型验证
        if iter % 500==0:
              model.eval()
              correct = 0
              total = 0
              for images, labels in test_loader:
                  images=images.view(-1,sequence_dim,input_dim).to(device)
                  outputs=model(images)
                  predict=torch.max(outputs.data,1)[1]
                  total+=labels.size(0)
                  if torch.cuda.is_available():
                      correct+=(predict.gpu()==labels.gpu()).sum()
                  else:
                      correct+=(predict==labels).sum()
              accuracy=correct/total*100
              loss_list.append(loss.data)
              accuracy_list.append(accuracy)
              iteration_list.append(iter)
              print("loss:{},loss:{},Accuracy:{}".format(iter,loss.item(),accuracy))
plt.plot(iteration_list,loss_list)
plt.xlabel("Number of Iterations")
plt.ylabel("Loss")
plt.title("RNN")
plt.show()

plt.plot(iteration_list, accuracy_list, color='r')
plt.xlabel("Number of iteration")
plt.ylabel("Accuracy")
plt.title("RNN")
plt.show()

滑动窗口CNN对时序数据分类

出处：2024湖南研赛A《使用智能手机记录人体活动状态》T2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
clc;
clear;
% 初始化参数
numActions = 12;
numTests = 5; % 每个动作的测试次数
dataDir = '附件2';
persons = {'Person4', 'Person5', 'Person6', 'Person7', 'Person8', ...
           'Person9', 'Person10', 'Person11', 'Person12', 'Person13'};
% persons=persons(1:4);
numPersons = numel(persons);
tableHeader = {"X轴加速度", "Y轴加速度", "Z轴加速度", ...
               "X轴角速度", "Y轴角速度", "Z轴角速度"};
windowSize = 600; % 窗口大小，可以根据需求调整
stride = 100; % 步长，窗口滑动的距离

% 初始化数据存储
X = [];
Y = [];

% 读取数据
for p = 1:numPersons
    personDir = fullfile(dataDir, persons{p});
    files = dir(fullfile(personDir, '*.xlsx'));
    
    for f = 1:numel(files)
        filename = files(f).name;
        filepath = fullfile(personDir, filename);
        
        % 读取表格数据
        table = readtable(filepath);
        data = table2array(table);
        fprintf('正在读取%s，长度%d\n', filepath,height(data));

        % 提取动作编号
        actionStr = regexp(filename, 'a(\d+)', 'tokens');
        action = str2double(actionStr{1}{1});
        
        numWindows=0;
        startIdx=1;
        endIdx=startIdx+windowSize-1;
        % numWindows = floor((size(data, 1) - windowSize) / stride) + 1; % 计算窗口数量
        
        % for j = 1:numWindows
        while true
            if endIdx > size(data, 1)
                break; % 确保窗口不超出数据范围
            end
            
            windowedData = data(startIdx:endIdx, :);
            
            X = cat(4, X, windowedData');
            Y = [Y; action];

            numWindows=numWindows+1;

            startIdx=startIdx+stride;
            endIdx=startIdx+windowSize-1;
        end
        
        fprintf("分为了%d个窗口数据\n",numWindows);


        % % 将数据添加到X和Y中
        % X = cat(4, X, data'); % 转置数据以匹配CNN输入格式
        % Y = [Y; a]; % 标签
    end
end

% 转换标签为分类
Y = categorical(Y);



%% 划分训练集、验证集和测试集
rng(42); % 设置随机种子，确保结果可重复
indices = randperm(size(X, 4));
% 计算划分点
train_size = floor(0.7 * size(X, 4));
val_size = floor(0.1 * size(X, 4));
% 划分
train_indices = indices(1:train_size);
val_indices = indices(train_size+1:train_size+val_size);
test_indices = indices(train_size+val_size+1:end);
% 分割
XTrain = X(:,:,:,train_indices);
YTrain = Y(train_indices);
XVal = X(:,:,:,val_indices);
YVal = Y(val_indices);
XTest = X(:,:,:,test_indices);
YTest = Y(test_indices);

fprintf('训练集大小: %d\n', numel(train_indices));
fprintf('验证集大小: %d\n', numel(val_indices));
fprintf('测试集大小: %d\n', numel(test_indices));

%% CNN
% 定义CNN网络架构
layers = [
    imageInputLayer([6, size(X, 2), 1], 'Name', 'input')
    
    convolution2dLayer([20, 3], 5, 'Padding', 'same', 'Name', 'conv1')
    batchNormalizationLayer('Name', 'batchnorm1')
    reluLayer('Name', 'relu1')
    
    convolution2dLayer([20, 3], 10, 'Padding', 'same', 'Name', 'conv2')
    batchNormalizationLayer('Name', 'batchnorm2')
    reluLayer('Name', 'relu2')
    
    maxPooling2dLayer([3, 4], 'Stride', [3, 4], 'Name', 'pool1')
    
    fullyConnectedLayer(200, 'Name', 'fc1')
    reluLayer('Name', 'relu3')
    
    fullyConnectedLayer(numActions, 'Name', 'fc2')
    softmaxLayer('Name', 'softmax')
    classificationLayer('Name', 'output')
];

% 修改训练选项
options = trainingOptions('adam', ...
    'MaxEpochs', 200, ...
    'MiniBatchSize', 64, ...
    'InitialLearnRate', 5e-3, ...
    'Shuffle', 'every-epoch', ...
    'ValidationData', {XVal, YVal}, ... % 添加验证数据
    'ValidationFrequency', 32, ... % 每30次迭代验证一次
    'Plots', 'training-progress', ...
    'Verbose', false);

% 训练网络（使用训练集，并在训练过程中验证）
net = trainNetwork(XTrain, YTrain, layers, options);

% 在测试集上评估网络
YPred = classify(net, XTest);
accuracy = sum(YPred == YTest) / numel(YTest);
fprintf('测试集准确率: %.2f%%\n', accuracy * 100);

%% 混淆矩阵

C = confusionmat(YTest, YPred);
% disp('混淆矩阵:');
% disp(C);
figure;
confusionchart(YTest, YPred);
title('CNN模型的混淆矩阵');
precision = diag(C) ./ sum(C, 1)';
recall = diag(C) ./ sum(C, 2);
f1_score = 2 * (precision .* recall) ./ (precision + recall);
% disp('各类别精确率:');
% disp(precision);
% disp('各类别召回率:');
% disp(recall);
% disp('各类别F1分数:');
% disp(f1_score);


overall_accuracy = sum(diag(C)) / sum(C(:));
fprintf('总体准确率: %.2f%%\n', overall_accuracy * 100);




%% 回代

YY = [];
YPred=[];

% 读取数据
for p = 1:numPersons
    personDir = fullfile(dataDir, persons{p});
    files = dir(fullfile(personDir, '*.xlsx'));
    
    for f = 1:numel(files)
        filename = files(f).name;
        filepath = fullfile(personDir, filename);
        
        % 读取表格数据
        table = readtable(filepath);
        data = table2array(table);
        fprintf('正在读取%s，长度%d\n', filepath,height(data));

        % 提取动作编号
        actionStr = regexp(filename, 'a(\d+)', 'tokens');
        action = str2double(actionStr{1}{1});
        
        numWindows=0;
        startIdx=1;
        endIdx=startIdx+windowSize-1;
        % numWindows = floor((size(data, 1) - windowSize) / stride) + 1; % 计算窗口数量
        
        % for j = 1:numWindows

        class=zeros(12,1);
        
        while true
            if endIdx > size(data, 1)
                break; % 确保窗口不超出数据范围
            end
            
            windowedData = data(startIdx:endIdx, :);
            
            % X = cat(4, X, windowedData');
           
            window_class=classify(net,windowedData');

            class(window_class)=class(window_class)+1;



            numWindows=numWindows+1;

            startIdx=startIdx+stride;
            endIdx=startIdx+windowSize-1;
        end
        
        fprintf("分为了%d个窗口数据\n",numWindows);

        YY = [YY; action];
        [~,Pred_index]=max(class);
        YPred=[YPred;Pred_index];


        % % 将数据添加到X和Y中
        % X = cat(4, X, data'); % 转置数据以匹配CNN输入格式
        % Y = [Y; a]; % 标签
    end
end

%% 回代混淆矩阵Y

C = confusionmat(YY, YPred);
% disp('混淆矩阵:');
% disp(C);
figure;
confusionchart(YY, YPred);
title('CNN模型回代混淆矩阵');
precision = diag(C) ./ sum(C, 1)';
recall = diag(C) ./ sum(C, 2);
f1_score = 2 * (precision .* recall) ./ (precision + recall);
disp('各类别精确率:');
disp(precision);
disp('各类别召回率:');
disp(recall);
disp('各类别F1分数:');
disp(f1_score);


overall_accuracy = sum(diag(C)) / sum(C(:));
fprintf('回代准确率: %.2f%%\n', overall_accuracy * 100);


%% 重测附件1

numPersons=3;
dataDir = '附件1';
persons = {'Person1', 'Person2', 'Person3'};
% 读取数据
ans1=zeros(3,60);
for p = 1:numPersons
    personDir = fullfile(dataDir, persons{p});
    files = dir(fullfile(personDir, '*.xlsx'));
    
    for SY = 1:60
        filename = strcat("SY",num2str(SY),".xlsx");
        filepath = fullfile(personDir, filename);
        
        % 读取表格数据
        table = readtable(filepath);
        data = table2array(table);
        fprintf('正在读取%s，长度%d\n', filepath,height(data));
        
        numWindows=0;
        startIdx=1;
        endIdx=startIdx+windowSize-1;
        % numWindows = floor((size(data, 1) - windowSize) / stride) + 1; % 计算窗口数量
        
        % for j = 1:numWindows

        class=zeros(12,1);
        
        while true
            if endIdx > size(data, 1)
                break; % 确保窗口不超出数据范围
            end
            
            windowedData = data(startIdx:endIdx, :);
            
            % X = cat(4, X, windowedData');
           
            window_class=classify(net,windowedData');

            class(window_class)=class(window_class)+1;



            numWindows=numWindows+1;

            startIdx=startIdx+stride;
            endIdx=startIdx+windowSize-1;
        end
        
        fprintf("分为了%d个窗口数据\n",numWindows);

        YY = [YY; action];
        [~,Pred_index]=max(class);
        YPred=[YPred;Pred_index];
        fprintf("预测为%s\n",YPred);

        ans1(p,SY)=YPred;

        % % 将数据添加到X和Y中
        % X = cat(4, X, data'); % 转置数据以匹配CNN输入格式
        % Y = [Y; a]; % 标签
    end
end


%% output ans1

writematrix("problem1_CNN.xlsx",ans1');


%% 测试附件3

%% 重测附件1

numPersons=3;
dataDir = '附件3';
% 读取数据
ans3=zeros(60,1);

for SY = 1:30
    filename = strcat("SY",num2str(SY),".xlsx");
    filepath = fullfile(personDir, filename);
    
    % 读取表格数据
    table = readtable(filepath);
    data = table2array(table);
    fprintf('正在读取%s，长度%d\n', filepath,height(data));
    
    numWindows=0;
    startIdx=1;
    endIdx=startIdx+windowSize-1;
    % numWindows = floor((size(data, 1) - windowSize) / stride) + 1; % 计算窗口数量
    
    % for j = 1:numWindows

    class=zeros(12,1);
    
    while true
        if endIdx > size(data, 1)
            break; % 确保窗口不超出数据范围
        end
        
        windowedData = data(startIdx:endIdx, :);
        
        % X = cat(4, X, windowedData');
       
        window_class=classify(net,windowedData');

        class(window_class)=class(window_class)+1;



        numWindows=numWindows+1;

        startIdx=startIdx+stride;
        endIdx=startIdx+windowSize-1;
    end
    
    fprintf("分为了%d个窗口数据\n",numWindows);

    YYY = [YYY; action];
    [~,Pred_index]=max(class);
    YPred=[YPred;Pred_index];
    fprintf("预测为%s\n",YPred);
    ans3(SY)=YPred;
end

Prompt

谁不用GPT呢？其实吧，我也是这么走过来的啊。这东西确实好用，但是希望在学习的差不多了之后，还是要摆脱对其的依赖性。并且注意，AI生成的东西一定要仔细甄别。

代码手

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
你是一位精通MATLAB编程的专家级AI助手。你具有以下特点和能力:

1. 对MATLAB语言的语法、函数和库有深入全面的了解。

2. 能够编写高效、简洁且易于理解的MATLAB代码。

3. 擅长解决数值计算、数据分析、信号处理、图像处理等领域的问题。

4. 熟悉MATLAB的各种工具箱,如Signal Processing Toolbox、Image Processing Toolbox等。

5. 能够提供详细的代码注释和解释,帮助用户理解代码的每个部分。

6. 善于优化MATLAB代码以提高运行效率。

7. 了解MATLAB编程的最佳实践和常见陷阱。

8. 能够根据用户的需求提供多种解决方案,并解释每种方案的优缺点。

9. 擅长调试MATLAB代码并提供错误修复建议。

10. 能够将复杂的数学概念转化为MATLAB代码。

11. 熟悉MATLAB的图形绘制功能,能创建各种类型的可视化图表。

当用户提出MATLAB相关的问题或要求时,请以专业、耐心和详细的方式回答,提供高质量的MATLAB代码和解释。如果需要更多信息,请礼貌地询问用户以便提供最准确的帮助。
但是在代码很长的情况下，尽量的给出需要解释或补充的代码片段，而不是直接给出完整的长代码。

论文手

1
2
3
4
5
6
7
8
9
10
11
你是一位数学建模和论文写作的专家，专注于将代码和建模思路转化为逻辑清晰、语言优美的学术论文。你擅长将提供的草稿和思路进行整理和优化，确保论文内容富有逻辑感和语文美感。同时，你熟练掌握各种数学模型和算法的实际步骤，能够将这些步骤用简洁或详细的文字进行准确表达。你的目标是撰写一篇完整且规范的学术论文，结构包括研究背景、问题描述、模型构建、算法步骤、实验设计、结果与讨论以及结论。请确保在写作过程中使用规范的学术语言，并适当引用相关文献，以增强论文的可信度和学术价值。
如果我需要你写的是论文片段的话，只需要提供片段即可。你也会需要完成一些简单任务，比如说论文润色。

在你回答我的时候，如果有公式的话，请尽量使用公式书写，也就是markdown的LaTex公式。我希望你使用美元符号（$）而不是其它符号（比如\[\]，这个不好）括起来的公式。如果是比较复杂的公式，或者多行公式，尽量多使用行间公式（也要使用双美元符号$$包含起来），并且如果你使用行间公式的话，一定要用\begin{align}\end{align}等括起来。不一定是align，这里只是作一个例子。下面再给你一个行间公式的例子：

$$
\begin{align}
v_n &= \sum_{i=0}^{n} a_i \Delta t \\
\theta_n &= \sum_{i=0}^{n} \omega_i \Delta t
\end{align}
$$

建模手

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
现在你需要充当数学建模中的建模手，负责模型搭建，提供团队对问题的解决思路和方法。你的主要职责将包括：

1. **理解和分析问题** - 你需要准确理解数学建模问题的本质和关键需求，以及如何从理论和实际角度进行分析。
2. **选择合适的模型** - 根据问题的性质选择最适合的数学模型，包括但不限于优化模型、预测模型、分类模型和评价模型。
3. **数据处理和分析** - 有效处理数据，运用统计方法分析数据，为模型构建提供必要的输入。
4. **构建和优化模型** - 构建初始模型，并通过测试和验证来优化它，确保模型的准确性和效率。
5. **模拟和预测** - 使用构建的模型进行必要的模拟和预测，提供问题的可能解决方案。
6. **结果解释和报告** - 清晰地解释模型的结果，以及这些结果如何对解决问题有帮助，确保能够被团队理解和接受。
7. **与团队协作** - 与编程手和论文手紧密合作，确保模型的实现和结果的有效传达。也就是说在关键性的时刻，你需要把大致的代码编写方向和论文写作注意事项要说出来，虽然不需要你具体的写作。
8. **持续学习和创新** - 在建模过程中不断学习最新的模型和技术，以提高问题解决的效率和创新性。

请开拓思路，多想一些数学模型，回答我的相关问题。

在你回答我的时候，如果有公式的话，请尽量使用公式书写，也就是markdown的LaTex公式。我希望你使用美元符号（$）而不是其它符号（比如\[\]，这个不好）括起来的公式。如果是比较复杂的公式，或者多行公式，尽量多使用行间公式（也要使用双美元符号$$包含起来），并且如果你使用行间公式的话，一定要用\begin{align}\end{align}等括起来。不一定是align，这里只是作一个例子。下面再给你一个行间公式的例子：

$$
\begin{align}
v_n &= \sum_{i=0}^{n} a_i \Delta t \\
\theta_n &= \sum_{i=0}^{n} \omega_i \Delta t
\end{align}
$$

翻译

1
2
您好！我需要您的帮助。您需要扮演一个翻译者和技术专家的双重角色。如果我给您中文，您需要翻译成英文；如果我给您英文，您需要翻译成中文。特别是，如果我给您的是中文或英文短语，您不仅需要翻译，还需要拓展讲解细节、语法重点等信息。
此外，您需要具备数学建模和计算机算法方面的专业知识。如果我给您相关领域的术语、概念或问题，您需要准确翻译，并提供详细的解释、背景信息以及实际应用的例子。请确保您的回答既专业又易于理解。