《数据结构》PTA作业合集

如何构造数据，使得两个字符串的hash值相等

数学建模竞赛(MCM)的方法与技巧。讲述了数据分析、优化建模和机理建模三大类题型的解题思路，以及论文写作的具体要求和注意事项。文章有关于数据探索、模型选择、算法实现等关键环节，并提供了一些比赛策略和时间规划的建议。*本随笔为数模国赛前的最后一堂课的笔记。有一些零零散散，但是信息量很大。如果有机会（现在是没必要啦），再整理成方便阅读的文字吧。

这部游戏好像挺出圈的，大多数人应该都知道剧情了吧。这次就不像上次的《LUNARiA》一样记录完整游玩过程了。从各个方面简单评论一下这部Galgame，记录自己的感受吧。

说实话，如果把饿殍定义为Galgame，那这故事背景真让我觉得有些过于沉重了……

也算是头一次在没有任何安利和剧透，仅在看了简介的情况下就直接下单并开始游玩一部gal了。果然，没有给我留下什么遗憾呢。

本文包含了数据处理、常用函数介绍、算法实现、绘图等模块，最后提供了一些完整实例。

VanillaGPT使用指南详细介绍了访问方法、登录步骤和模型选择策略。重点强调密钥的重要性和保密性，并对比了多种GPT模型的性能、用途和价格。推荐使用gpt-4-turbo-2024-04-09、gpt-4o和gpt-4o-mini三种模型，分别适用于正式用途、中型问题和小型问题。指南旨在帮助用户根据具体需求选择最合适的模型，以实现高效且经济的使用体验。

本文详细介绍了在华为Matebook e 2022上安装Arch Linux双系统的全过程，包括准备工作、系统安装、网络配置、驱动安装等关键步骤。文章从BIOS设置入手，逐步指导读者如何配置网络，分区，安装系统核心组件，以及如何设置启动管理器GRUB。此外，还涵盖了系统优化、桌面环境安装和必要的后续配置，确保用户能够顺利完成安装并享受Arch Linux。

2023多波束测线问题

问题一模型建立与求解

第一问是一个平面几何题，两篇优秀论文方法和答案都差不多，就不分开讲述了。当海底面为一个与水平面夹角为α的坡面，且测线方向与水平面平行时，那么每条测线与海底面的交线均为海底面的等高线，结合解析几何相关知识，可以建立计算多波束测深的覆盖宽度模型以及计算相邻条带之间重叠率的模型。

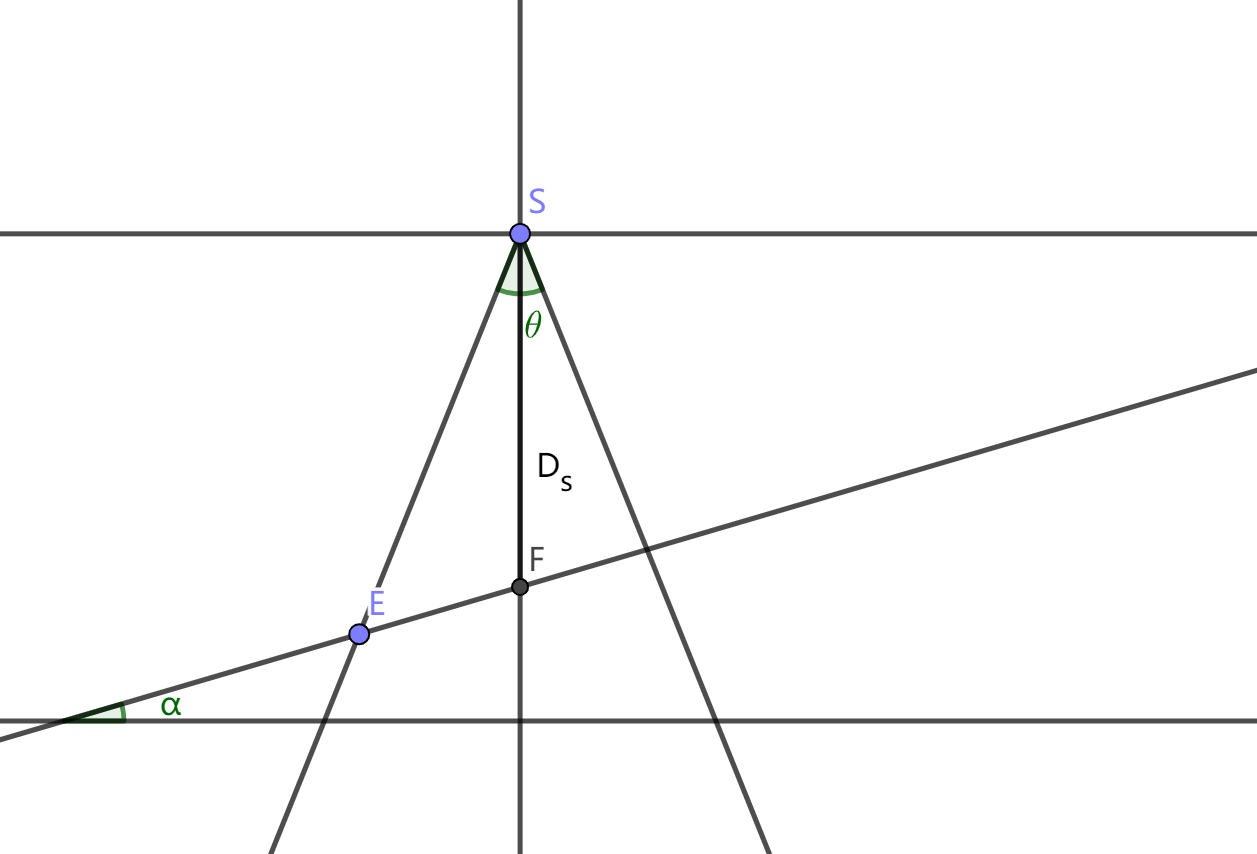
确定已知量：\(\alpha,\theta,D_{s0},d\)

软件版本

• MATLAB R2023b
• yalmip 2021-03-31
• CPLEX 12.10

不求新，但求适配。此版本组合经过我在两台电脑上成功安装